
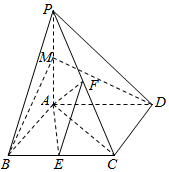
 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角45°,E,F,M分别是BC,PC,PA的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角45°,E,F,M分别是BC,PC,PA的中点.分析 (1)取AC中点O,连结OM,利用中位线定理得出OM∥PC,故而PC∥平面MBD;
(2)由PA⊥平面ABCD得PA⊥AE,由菱形的性质得出AE⊥BC,故而AE⊥AD,于是AE⊥平面PAD,故而AE⊥PD;
(3)建立空间坐标系,使用向量法解出;
(4)以△ACD为底面,PA为棱锥的高,代入棱锥的体积公式计算.
解答 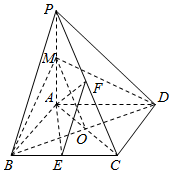 (1)证明:连结BD交AC与O,连结MO
(1)证明:连结BD交AC与O,连结MO
∵四边形ABCD是菱形,∴O是AC的中点,又M是PA的中点,
∴MO∥PC,∵MO?平面MBD,PC?平面MBD,
∴PC∥平面MBD.
(2)证明:∵PA⊥平面ABCD,AE?平面ABCD,
∴PA⊥AE,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,BC∥AD,
∵E是BC中点,∴AE⊥BC,
∴AE⊥AD,又PA∩AD=A,PA?平面PAD,AD?平面PAD
∴AE⊥平面PAD,∵PD?平面PAD,
∴AE⊥PD.
(3)解:以A为坐标原点建立如图所示的空间直角坐标系,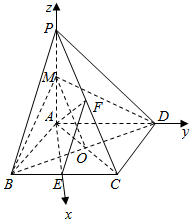
:∵PA⊥平面ABCD,∴∠PCA为直线PC与平面ABCD所成的角,
∴∠PCA=45°.∴PA=AC,
设AB=a,则A(0,0,0),E($\frac{\sqrt{3}a}{2}$,0,0),C($\frac{\sqrt{3}a}{2}$,$\frac{a}{2}$,0),P(0,0,a),∴F($\frac{\sqrt{3}a}{4}$,$\frac{a}{4}$,$\frac{a}{2}$).
∴$\overrightarrow{AE}$=($\frac{\sqrt{3}a}{2}$,0,0),$\overrightarrow{AF}$=($\frac{\sqrt{3}a}{4}$,$\frac{a}{4}$,$\frac{a}{2}$),$\overrightarrow{AC}$=($\frac{\sqrt{3}a}{2}$,$\frac{a}{2}$,0),
设平面AEF的法向量为$\overrightarrow{{n}_{1}}$=(x,y,z),则$\overrightarrow{{n}_{1}}•\overrightarrow{AE}=0$,$\overrightarrow{{n}_{1}}•\overrightarrow{AF}$=0,
∴$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}ax=0}\\{\frac{\sqrt{3}}{4}ax+\frac{1}{4}ay+\frac{1}{2}az=0}\end{array}\right.$,令z=1得$\overrightarrow{{n}_{1}}$=(0,-2,1).
设平面ACF的法向量为$\overrightarrow{{n}_{2}}$=(x,y,z),则$\overrightarrow{{n}_{2}}•\overrightarrow{AF}=0$,$\overrightarrow{{n}_{2}}•\overrightarrow{AC}=0$,
∴$\left\{\begin{array}{l}{\frac{\sqrt{3}ax}{4}+\frac{ay}{4}+\frac{az}{2}=0}\\{\frac{\sqrt{3}ax}{2}+\frac{ay}{2}=0}\end{array}\right.$,令x=1得$\overrightarrow{{n}_{2}}$=(1,-$\sqrt{3}$,0).
∴$\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}$=2$\sqrt{3}$,|$\overrightarrow{{n}_{1}}$|=$\sqrt{5}$,|$\overrightarrow{{n}_{2}}$|=2,
∴cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{\sqrt{15}}{5}$.
∴二面角E-AF-C的余弦值为$\frac{{\sqrt{15}}}{5}$.
(4)解:∵PA⊥平面ABCD,∴∠PCA为直线PC与平面ABCD所成的角,
∴∠PCA=45°,∴AC=PA=2,
∴S△ACD=$\frac{\sqrt{3}}{4}A{C}^{2}$=$\sqrt{3}$.
∴VC-PAD=VP-ACD=$\frac{1}{3}{S}_{△ACD}•PA$=$\frac{1}{3}×\sqrt{3}×2$=$\frac{{2\sqrt{3}}}{3}$.
点评 本题考查了线面平行与垂直的性质与判定,空间角的计算和棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
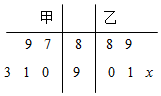 如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.
如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米.该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元/平方米):
某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米.该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元/平方米):| 房号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
| B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8. | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,+∞) | C. | (1,$\root{3}{4}$) | D. | ($\root{3}{4}$,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com