
| A. | $(0,\frac{6}{e^3})$ | B. | $(-3,\frac{6}{e^3})$ | C. | $(-2e,\frac{6}{e^3})$ | D. | (0,2e) |
分析 设f(x)与g(x)的共同切线的切点为(x0,y0),根据导数求出切点,即可求出m的值,结合图象可知m的取值范围.
解答 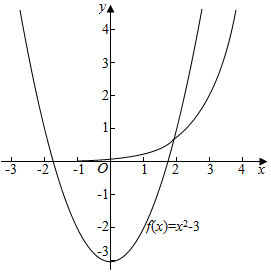 解:设f(x)与g(x)的共同切线的切点为(x0,y0),
解:设f(x)与g(x)的共同切线的切点为(x0,y0),
∵f(x)=x2-3,g(x)=mex,
∴f′(x)=2x,g(x)=mex,
∴f′(x0)=g′(x0),f(x0)=g(x0),
∴2x0=$m{e}^{{x}_{0}}$,x02-3=$m{e}^{{x}_{0}}$,
∴x0=x02-3,
解得x0=3,或x0=-1(舍去)
当x0=3,
∴6=me3,即m=$\frac{6}{{e}^{3}}$,
∵方程f(x)=g(x)有三个不同的实根,由图象可知,
∴0<m<$\frac{6}{{e}^{3}}$,
故选:A.
点评 本题主要考查了利用导数研究函数的极值,以及函数与方程的思想,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
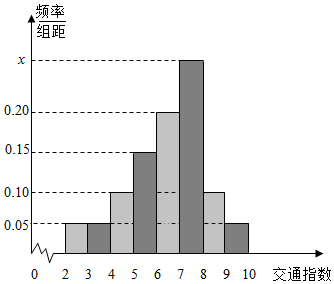 交通指数是指交通拥堵指数或交通运行指数(Traffic Performance Index,即“TPI”),是反应道路畅通或拥堵的概念性数值,交通指数的取值范围为0~10,分为五级:0~2畅通,2~4为基本畅通,4~6轻度畅通,6~8为中度拥堵,8~10为严重拥堵.高峰时段,巴中市交通指挥中心随机选取了市区40个交通路段,依据交通指数数据绘制的频率分布直方图如图所示:
交通指数是指交通拥堵指数或交通运行指数(Traffic Performance Index,即“TPI”),是反应道路畅通或拥堵的概念性数值,交通指数的取值范围为0~10,分为五级:0~2畅通,2~4为基本畅通,4~6轻度畅通,6~8为中度拥堵,8~10为严重拥堵.高峰时段,巴中市交通指挥中心随机选取了市区40个交通路段,依据交通指数数据绘制的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | [-2,2] | C. | [-∞,2] | D. | [0,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com