
分析 (1)由周期求得ω,由函数g(x)为奇函数求得φ和b的值,从而得到函数f(x)的解析式.
(2)令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈z,求得x的范围,即可得到函数的减区间,令2x+$\frac{π}{3}$=kπ,k∈z,求得x,即可解得函数的对称中心.
解答 解:(1)∵$\frac{2π}{ω}$=2×$\frac{π}{2}$,∴ω=2,∴f(x)=sin(2x+φ)-b.
又g(x)=sin[2(x-$\frac{π}{6}$)+φ]-b+$\sqrt{3}$为奇函数,且0<φ<π,则φ=$\frac{π}{3}$,b=$\sqrt{3}$,
故f(x)=sin(2x+$\frac{π}{3}$)-$\sqrt{3}$.
(2)令2x+$\frac{π}{3}$=kπ,k∈z,求得:x=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z,
故函数的对称中心为:($\frac{kπ}{2}$-$\frac{π}{6}$,-$\sqrt{3}$),k∈Z,
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈z,求得:$\frac{π}{12}$+kπ≤x≤$\frac{7π}{12}$+kπ,(k∈Z),
故函数的减区间为[$\frac{π}{12}$+kπ,$\frac{7π}{12}$+kπ](k∈Z).
点评 本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,正弦函数的单调性,函数y=Asin(ωx+φ)的图象变换,函数的奇偶性,考查了数形结合思想的应用,属于中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{6}{e^3})$ | B. | $(-3,\frac{6}{e^3})$ | C. | $(-2e,\frac{6}{e^3})$ | D. | (0,2e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | $(-∞,\frac{1}{2}]∪(1,2]$ | C. | (0,2] | D. | $(0,\frac{1}{2}]∪(1,2]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
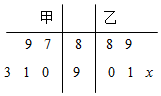 如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.
如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米.该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元/平方米):
某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米.该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元/平方米):| 房号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
| B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8. | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{17}{8}$,+∞) | B. | (-∞,$\frac{17}{8}$] | C. | (-∞,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com