
【题目】选修4—5:不等式选讲
已知函数f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集为{x|-2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m-f(-n)成立,求实数m的取值范围.
【答案】(1) a=1 (2)[4,+∞).
【解析】
试题分析:(1)根据方程的解与不等式解集关系得:-2 ,3为|2x-a|+a =6两根,解得a=1。也可先利用绝对值定义求不等式解集a-3≤x≤3,再根据同解得等量关系a-3=-2 (2)不等式有解问题,一般转化为对应函数最值问题:f(n)+f(-n) 最小值≤m,再利用绝对值定义求f(n)+f(-n) =|2n-1|+|2n+1|+2最小值,也可利用绝对值三角不等式求最小值:|2n-1|+|2n+1|![]()
试题解析:(1)由|2x-a|+a≤6,得|2x-a|≤6-a,
∴a-6≤2x-a≤6-a,即a-3≤x≤3,∴a-3=-2,∴a=1
(2)由(1)知f(x)=|2x-1|+1,
令φ(n)=f(n)+f(-n),
则φ(n)=|2n-1|+|2n+1|+2
=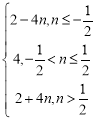
∴φ(n)的最小值为4,故实数m的取值范围是[4,+∞).


科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
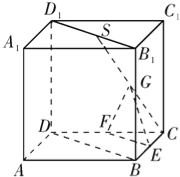
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某初级中学有三个年级,各年级男、女生人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 | z | 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求z的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,将该样本看成一个总体,从中任选2名学生,求至少有1名女生的概率;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上.
的图像上.
(I)求数列![]() 的首项
的首项![]() 和通项公式
和通项公式![]() ;
;
(II)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(III)已知数列![]() 满足
满足![]() .若对任意
.若对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于某设备的使用年限![]() 和所支出的维修费用
和所支出的维修费用![]() (万元),有如下的统计资料:
(万元),有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)如由资料可知![]() 对
对![]() 呈线形相关关系.试求:线形回归方程;(
呈线形相关关系.试求:线形回归方程;(![]() ,
, )
)
(2)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果袋中装有数量差别很大而大小相同的白球和黄球(只是颜色不同)若干个,从中任取一球,取了10次有7个白球,估计袋中数量最多的是________球.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.

(1) 证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当
的图象.当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com