
分析 (1)根据真数大于0,解不等式求出A,根据对勾函数的图象和性质,求出集合B,进而可得A∩B;
(2)根据(1)先求出∁RA,再由C⊆∁RA对a进行分类讨论,可得a的取值范围.
解答 解:(1)由-x2-2x+8>0得:x∈(-4,2),
∴A=(-4,2),
由y=x+$\frac{1}{x+1}$=x+1+$\frac{1}{x+1}$-1∈(-∞,-3]∪[1,+∞),
∴B=(-∞,-3]∪[1,+∞),
∴A∩B=(-4,-3]∪[1,2),
(2)∁RA=(-∞,-4]∪[2,+∞),
解ax2+(4a-$\frac{1}{a}$)x-$\frac{4}{a}$=0得:x=-4,或x=$\frac{1}{{a}^{2}}$,
当a>0时,解不等式ax2+(4a-$\frac{1}{a}$)x-$\frac{4}{a}$≤0得:x∈[-4,$\frac{1}{{a}^{2}}$],不满足C⊆∁RA,
当a<0时,解不等式ax2+(4a-$\frac{1}{a}$)x-$\frac{4}{a}$≤0得:x∈(-∞,-4]∪[$\frac{1}{{a}^{2}}$,+∞),
由C⊆∁RA得:$\frac{1}{{a}^{2}}$≥2,解得:a∈[$-\frac{\sqrt{2}}{2}$,0),
∴a的取值范围为[$-\frac{\sqrt{2}}{2}$,0)
点评 本题考查的知识点是集合的交集,补集运算和集合的关系,函数的定义域,值域,解二次不等式,是集合,函数,不等式的综合应用,难度中档.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 15 | C. | 5 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
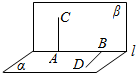 如图,已知α∩β=l,A∈l,B∈l,(A,B不重合),过A在平面α内做直线AC,过B在平面α内做直线BD.求证:AC,BD是异面直线.
如图,已知α∩β=l,A∈l,B∈l,(A,B不重合),过A在平面α内做直线AC,过B在平面α内做直线BD.求证:AC,BD是异面直线.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com