
如图,在四棱柱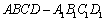 中,
中,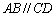 ,
, ,且
,且 .
.
(1)求证: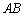 ∥平面
∥平面 ;
;
(2)求证: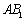 ⊥平面
⊥平面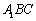 .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
已知数列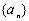 满足
满足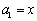 ,
,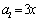 ,
,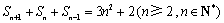 ,
,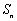 是数列
是数列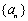 的前
的前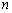 项和.
项和.
(1)若数列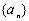 为等差数列.
为等差数列.
(ⅰ)求数列的通项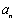 ;
;
(ⅱ)若数列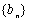 满足
满足 ,数列
,数列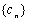 满足
满足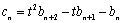 ,试比较数列
,试比较数列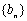 前
前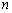 项和
项和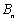 与
与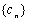 前
前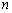 项和
项和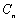 的大小;
的大小;
(2)若对任意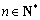 ,
,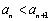 恒成立,求实数
恒成立,求实数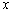 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查.现将800名学生从1到800进行编号.已知从33~48这16个数中取的数是39,则在第1小组1~16中随机抽到的数是( )
A.5 B.7 C.11 D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点 (0,-2),椭圆
(0,-2),椭圆 :
: 的离心率为
的离心率为 ,
, 是椭圆的焦点,直线
是椭圆的焦点,直线 的斜率为
的斜率为 ,
, 为坐标原点.
为坐标原点.
(1) 求 的方程;
的方程;
(2) 设过点 的直线
的直线 与
与 相交于
相交于 两点,当
两点,当 的面积最大时,求
的面积最大时,求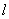 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com