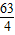设二次函数f(x)=ax2+bx+c在区间[-2,2]上的最大值、最小值分别为M、m,集合A={x|f(x)=x}.
(1)若A={1,2},且f(0)=2,求M和m的值;
(2)若A={2},且a≥1,记g(a)=M-m,求g(a)的最小值.
【答案】
分析:(1)先求得c=0;若A={1,2},则说明f(x)-x=0两根为1,2.利用韦达定理求a,b,再利用二次函数图象与性质求解.
(2)若A={2},得到方程f(x)-x=0有两个相等的解都为2,根据韦达定理求出a,b,c的关系式,根据a大于等于1,利用二次函数求最值的方法求出在[-2,2]上的m和M,代入g(a)=m+M中得到新的解析式g(a)根据g(a)的在[1,+∞)上单调增,求出g(a)的最小值为g(1),求出值即可.
解答:解:(1)∵f(0)=2,∴c=2
∵A={1,2},∴ax
2+(b-1)x+2=0有两根为1,2.
由韦达定理得,
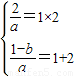
∴
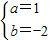
∴f(x)=x
2-2x+2
∵x∈[-2,2],∴M=f(-2)=10,m=f(1)=1
(2)若A={2},方程ax
2+(b-1)x+c=0有两相等实根x
1=x
2=2,
根据韦达定理得到:2+2=-
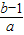
,2×
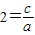
,所以c=4a,b=1-4a,
∴f(x)=ax
2+bx+c=ax
2+(1-4a)x+4a,x∈[-2,2]
其对称轴方程为x=
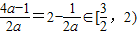
∴M=f(-2)=16a-2,m=f(2-
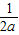
)=2-
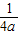
则g(a)=M+m=16a-2+2-
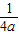
=16-
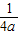
又g(a)在区间[1,+∞)上为单调递增的,
∴当a=1时,g(a)
min=16-

=
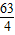 点评:
点评:查学生灵活运用韦达定理解决实际问题,掌握利用数形结合法解决数学问题,会求一个闭区间上二次函数的最值.

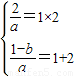 ∴
∴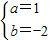
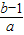 ,2×
,2×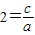 ,所以c=4a,b=1-4a,
,所以c=4a,b=1-4a,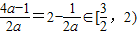
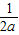 )=2-
)=2-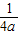
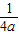 =16-
=16-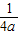
 =
=