
分析 (I)设点P(x',y'),点M的坐标为(x,y),由题意可知$\left\{\begin{array}{l}x'=x\\ y'=2y\end{array}\right.$,由此能求出点M的轨迹C的方程.
(II)设点A(x1,y1),B(x2,y2),点N的坐标为(x0,y0),当直线l与x轴重合时,线段AB的中点N就是原点O,不合题意;设直线l:$x=my+\sqrt{3}$,由$\left\{\begin{array}{l}x=my+\sqrt{3}\\{x^2}+4{y^2}=4\end{array}\right.$,得$({m^2}+4){y^2}+2\sqrt{3}my-1=0$,由此利用韦达定理、向量相等、直线方程,结合已知条件能证明$\overrightarrow{OE}$=$2\overrightarrow{ON}$的充要条件是|AB|=3.
解答 解:(I)设点P(x',y'),点M的坐标为(x,y),
由题意可知$\left\{\begin{array}{l}x'=x\\ y'=2y\end{array}\right.$…(2分)
又x'2+y'2=4,∴${x^2}+4{y^2}=4⇒\frac{x^2}{4}+{y^2}=1$.
所以点M的轨迹C的方程为$\frac{x^2}{4}+{y^2}=1$…(4分)
证明:(II)设点A(x1,y1),B(x2,y2),点N的坐标为(x0,y0),
(i)当直线l与x轴重合时,线段AB的中点N就是原点O,不合题意,舍去…(5分)(ii)设直线l:$x=my+\sqrt{3}$,
由$\left\{\begin{array}{l}x=my+\sqrt{3}\\{x^2}+4{y^2}=4\end{array}\right.$消去x,
得$({m^2}+4){y^2}+2\sqrt{3}my-1=0$,
∴${y_0}=-\frac{{\sqrt{3}m}}{{{m^2}+4}}$…(6分)
∴${x_0}=m{y_0}+\sqrt{3}=-\frac{{\sqrt{3}{m^2}}}{{{m^2}+4}}+\frac{{\sqrt{3}{m^2}+4\sqrt{3}}}{{{m^2}+4}}=\frac{{4\sqrt{3}}}{{{m^2}+4}}$
∴点N的坐标为$(\frac{{4\sqrt{3}}}{{{m^2}+4}},-\frac{{\sqrt{3}m}}{{{m^2}+4}})$,…(8分)
①若$\overrightarrow{OE}$=$2\overrightarrow{ON}$,则点E的坐标为$(\frac{{8\sqrt{3}}}{{{m^2}+4}},-\frac{{2\sqrt{3}m}}{{{m^2}+4}})$,由点E在曲线C上,
得$\frac{48}{{{{({m^2}+4)}^2}}}+\frac{{12{m^2}}}{{{{({m^2}+4)}^2}}}=1$,即m4-4m2-32=0,∴m2=8(m2=-4舍去).
由方程①得$|y{\;}_1-{y_2}|=\frac{{\sqrt{12{m^2}+4{m^2}+16}}}{{{m^2}+4}}=\frac{{4\sqrt{{m^2}+1}}}{{{m^2}+4}}=1$,
又|x1-x2|=|my1-my2|=|m(y1-y2)|,
∴$|AB|=\sqrt{{m^2}+1}|{y_1}-{y_2}|=3$…(10分)
②若|AB|=3,由①得$\frac{{4({m^2}+1)}}{{{m^2}+4}}=3$,∴m2=8.
∴点N的坐标为$(\frac{{\sqrt{3}}}{3},±\frac{{\sqrt{6}}}{6})$,射线ON方程为$y=±\frac{{\sqrt{2}}}{2}x(x>0)$
由$\left\{\begin{array}{l}y=±\frac{{\sqrt{2}}}{2}x(x>0)\\{x^2}+4{y^2}=4\end{array}\right.$解得$\left\{\begin{array}{l}x=\frac{{2\sqrt{3}}}{3}\\ y=±\frac{{\sqrt{6}}}{3}\end{array}\right.$∴点E的坐标为$(\frac{{2\sqrt{3}}}{3},±\frac{{\sqrt{6}}}{3})$,
∴$\overrightarrow{OE}$=$2\overrightarrow{ON}$.
综上,$\overrightarrow{OE}$=$2\overrightarrow{ON}$的充要条件是|AB|=3…(12分)
点评 本题考查曲线方程的求法,考查充要条件的证明,是中档题,解题时要认真审题,注意韦达定理、向量相等、直线方程等知识点和等价转化思想的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{10}{3}$ | C. | $\sqrt{10}$ | D. | $\frac{2\sqrt{7}+5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
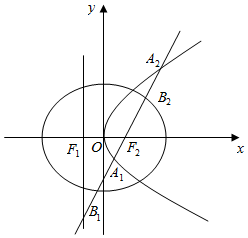 设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2,椭圆C2以F1,F2为焦点且椭圆C2上的点到F1的距离的最大值为3.
设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2,椭圆C2以F1,F2为焦点且椭圆C2上的点到F1的距离的最大值为3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2$\sqrt{2}$-1,2$\sqrt{2}$-1] | B. | [-2$\sqrt{2}$-1,2$\sqrt{2}$-1) | C. | [-$\sqrt{5}$-1,$\sqrt{5}$-1] | D. | [-$\sqrt{5}$-1,$\sqrt{5}$-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | ±$\sqrt{3}$ | C. | ±$\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com