
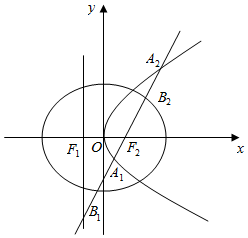
 ��������C1��y2=4x������x�ύ�ڵ�F1������ΪF2����ԲC2��F1��F2Ϊ��������ԲC2�ϵĵ㵽F1�ľ�������ֵΪ3��
��������C1��y2=4x������x�ύ�ڵ�F1������ΪF2����ԲC2��F1��F2Ϊ��������ԲC2�ϵĵ㵽F1�ľ�������ֵΪ3������ ��1���������֪C=1��a+c=3���������a��b��c��ֵ�����������Բ�ı����̣�
��2�����൱б�ʲ�����ʱ���жϲ���������б�ʴ��ڣ����ֱ�߷��̣���ֱ�߷��̴�����Բ���̣��õ�����x��һԪ���η��̣���Τ�ﶨ����Բ�����ʡ��ҳ���ʽ�����|A1A2|��
��3����ԲN�ķ���Ϊ����x+1��2+y2=16�����Բ�ģ��������ߵ����ʣ������|MF1|=4-|MF2|����Բ�����У�
��� �⣺��1����������C1��y2=4x������x�ύ�ڵ�F1������ΪF2��
����ԲC2�Ľ�������ΪF1��-1��0����F2��1��0����
����ԲC2�ķ���Ϊ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$��a��b��0����
�������$\left\{\begin{array}{l}{c=1}\\{a+c=3}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����a=2��c=1��b=$\sqrt{3}$������Բ�ı�����Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$������3�֣�
��2����ֱ��l��x�ᴹֱʱ��B1��1��$\frac{3}{2}$����B2��1��-$\frac{3}{2}$����
��F1��-1��0������ʱ$\overrightarrow{{B}_{1}{F}_{1}}$•$\overrightarrow{{B}_{2}{F}_{1}}$��0��
����B1B2Ϊֱ����Բ������F1��������������
��ֱ��l����x�ᴹֱʱ����ֱ��l�ķ���Ϊ��y=k��x-1����
��$\left\{\begin{array}{l}{y=k��x-1��}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$������3+4k2��x2+8k2x+4k2-12=0��
�߽�������Բ�ڲ���������������㣬
��B1��x1��y1����B2��x2��y2������x1+x2=-$\frac{8{k}^{2}}{3+4{k}^{2}}$��x1•x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$��
����B1B2Ϊֱ����Բ����F1��
��$\overrightarrow{{B}_{1}{F}_{1}}$•$\overrightarrow{{B}_{2}{F}_{1}}$=0����F1��-1��0����
�ࣨ-1-x1��•��-1-x2��+y1y2=0��
�ࣨ1+k2��x1x2+��1-k2����x1+x2��+1+k2=0��
�ࣨ1+k2��•$\frac{4{k}^{2}-12}{3+4{k}^{2}}$+��1-k2��•��-$\frac{8{k}^{2}}{3+4{k}^{2}}$��+1+k2=0��
���k2=$\frac{9}{7}$��
��$\left\{\begin{array}{l}{y=k��x-1��}\\{{y}^{2}=4x}\end{array}\right.$����k2x2-��2k2+4��x+k2=0��
��ֱ��l�����������������㣬
��k��0����A1��x3��y3����A2��x4��y4������x3+x4=$\frac{2{k}^{2}+4}{{k}^{2}}$=2+$\frac{4}{{k}^{2}}$��x3x4=1��
��|A1A2|=x3+x4+p=2+$\frac{4}{{k}^{2}}$+2=$\frac{64}{9}$������8�֣�
��3�����ڶ�ԲN��ʹ�á�M���N�����У�
��ԲN�ķ���Ϊ����x+1��2+y2=16��Բ������F��-1��0����
����Բ����֪|MF1|+|MF2|=2a=4��
��|MF1|=4-|MF2|��
����Բ�����У� ����12�֣�
���� ���⿼����Բ�ı����̵��������ҳ���������ʱҪע������б�ʽ��Τ�ﶨ����Բ�����ʡ��ҳ���ʽ�ĺ������ã��������⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$ | B�� | $\sqrt{17}$ | C�� | 3$\sqrt{2}$ | D�� | $\sqrt{33}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 25�� | B�� | 36�� | C�� | 49�� | D�� | 32�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{5}\sqrt{6}$ | B�� | $\frac{3}{5}\sqrt{6}$ | C�� | $\frac{4}{5}\sqrt{6}$ | D�� | $\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
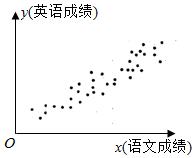 Ϊ�о����ijɼ���Ӣ��ɼ�֮���Ƿ����������ع�ϵ��ͳ�����Ƴɼ��õ���ͼ��ʾ��ɢ��ͼ���������ᵥλ������ͬ�����ûع�ֱ��$\hat y$=$\hat b$x+$\hat a$���Ƶؿ̻������ϵ������ͼ�Σ����½������п��ܳ������ǣ�������
Ϊ�о����ijɼ���Ӣ��ɼ�֮���Ƿ����������ع�ϵ��ͳ�����Ƴɼ��õ���ͼ��ʾ��ɢ��ͼ���������ᵥλ������ͬ�����ûع�ֱ��$\hat y$=$\hat b$x+$\hat a$���Ƶؿ̻������ϵ������ͼ�Σ����½������п��ܳ������ǣ�������| A�� | ������ع�ϵ��ǿ��b��ֵΪ3.25 | B�� | ������ع�ϵ��ǿ��b��ֵΪ0.83 | ||
| C�� | ������ع�ϵ��ǿ��b��ֵΪ-0.87 | D�� | ������ع�ϵ̫�������о���ֵ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com