
| A. | (-1,+∞) | B. | (3,+∞) | C. | (-∞,-1) | D. | (-∞,-5) |
分析 由真数大于0求出原函数的定义域,然后求出内函数的减区间得答案.
解答 解:由x2+2x-15>0,得x<-5或x>3.
∴函数$f(x)={log_{\frac{1}{2}}}({x^2}+2x-15)$的定义域为(-∞,-5)∪(3,+∞).
令t=x2+2x-15,则外层函数为y=$lo{g}_{\frac{1}{2}}t$,是减函数,
又内层函数t=x2+2x-15的减区间为(-∞,-5),
∴函数$f(x)={log_{\frac{1}{2}}}({x^2}+2x-15)$的单调递增区间是(-∞,-5).
故选:D.
点评 本题主要考查了复合函数的单调性以及单调区间的求法.对应复合函数的单调性,一要注意先确定函数的定义域,二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断,判断的依据是“同增异减”,是中档题.


科目:高中数学 来源: 题型:填空题
 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
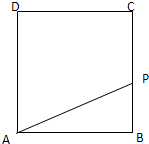 动点P从边长为1的正方形ABCD的顶点A出发顺次经过B,C,D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.
动点P从边长为1的正方形ABCD的顶点A出发顺次经过B,C,D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4) | B. | (0,4] | C. | (0,2] | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com