
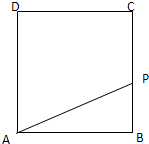
 动点P从边长为1的正方形ABCD的顶点A出发顺次经过B,C,D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.
动点P从边长为1的正方形ABCD的顶点A出发顺次经过B,C,D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.分析 (1)动点P各有不同位置,计算PA也有不同的方法,因此同样必须对P点的位置进行分类求解.
(2)△ABP的形状各有特征,计算它们的面积也有不同的方法,因此同样必须对P点的位置进行分类求解.
解答 解:(1)如原题图,当P在AB上运动时,PA=x;
当P点在BC上运动时,由Rt△ABD?可得PA=$\sqrt{1+(x-1)^{2}}$
当P点在CD上运动时,由Rt△ADP易得PA=$\sqrt{1+(3-x)^{2}}$
当P点在DA上运动时,PA=4-x,
故f(x)的表达式为:
f(x)=$\left\{\begin{array}{l}{x,(0≤x≤1)}\\{\sqrt{{x}^{2}-2x+2},(1<x≤2)}\\{\sqrt{{x}^{2}-6x+10},(2<x≤3)}\\{4-x,(3<x≤4)}\end{array}\right.$.
(2)g(x)的简图:
由于P点在折线ABCD上不同位置时,如原题图,
当P在线段AB上时,即0≤x<1时,S△ABP的面积S=0;
当P在线段BC上时,即1<x≤2时,S△ABP=$\frac{1}{2}$AB•BP=$\frac{1}{2}$(x-1);
当P在线段CD上时,即2<x≤3时,S△ABP=$\frac{1}{2}$•1•1=$\frac{1}{2}$
当P在线段DA上时,即3<x≤4时,S△ABP=$\frac{1}{2}$(4-x)
故g(x)=$\left\{\begin{array}{l}{0,(0≤x≤1)}\\{\frac{1}{2}(x-1),(1<x≤2)}\\{\frac{1}{2},(2<x≤3)}\\{\frac{1}{2}(4-x),(3<x≤4)}\end{array}\right.$.
点评 本题考查了分段函数的求法,背景是动点的轨迹不同,线段的长以及三角形的面积也会发生变化.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+3y+4=0 | B. | 2x+3y-8=0 | C. | 3x-2y-7=0 | D. | 3x-2y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (3,+∞) | C. | (-∞,-1) | D. | (-∞,-5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com