
分析 (1)由已知可求范围$θ+\frac{π}{4}∈(\frac{3π}{4},\frac{5π}{4})$,利用同角三角函数基本关系式可求所以cos(θ+$\frac{π}{4}$),利用两角差的正弦函数公式及特殊角的三角函数值即可计算得解.
(2)由已知及两角和的余弦函数公式,同角三角函数基本关系式可得$cosαcosβ-sinαsinβ=\frac{1}{3}$,$sinαsinβ=\frac{1}{3}cosαcosβ$,联立可解得$cosαcosβ=\frac{1}{2}$,进而利用两角差的余弦函数公式即可得解.
解答 (本题满分为14分)
解:(1)因为$θ∈(\frac{π}{2},π)$,
所以$θ+\frac{π}{4}∈(\frac{3π}{4},\frac{5π}{4})$,…(2分)
所以$cos(θ+\frac{π}{4})=-\sqrt{1-{{sin}^2}(θ+\frac{π}{4})}=-\frac{{2\sqrt{2}}}{3}$,…(4分)
所以$sinθ=sin[(θ+\frac{π}{4})-\frac{π}{4}]=sin(θ+\frac{π}{4})cos\frac{π}{4}-cos(θ+\frac{π}{4})sin\frac{π}{4}=\frac{{4+\sqrt{2}}}{6}$.
(2)由$cos(α+β)=\frac{1}{3}$,得:$cosαcosβ-sinαsinβ=\frac{1}{3}$,①
由$tanα•tanβ=\frac{1}{3}$,得:$\frac{sinαsinβ}{cosαcosβ}=\frac{1}{3}$,即$sinαsinβ=\frac{1}{3}cosαcosβ$,②
由①、②得$cosαcosβ=\frac{1}{2}$,
所以$cos(α-β)=cosαcosβ+sinαsinβ=\frac{4}{3}cosαcosβ=\frac{2}{3}$.…(14分)
点评 本题主要考查了同角三角函数基本关系式,两角和与差的正弦函数、余弦函数公式及特殊角的三角函数值在三角函数化简求值中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2} | B. | {-2,0,2} | C. | {0,2,4} | D. | {-2,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x2+1 | B. | y=lg|x| | C. | $y=\frac{1}{x}$ | D. | y=e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M、N、P | B. | M、P、Q | C. | N、P、Q | D. | M、N、Q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
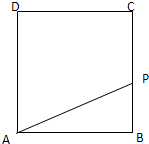 动点P从边长为1的正方形ABCD的顶点A出发顺次经过B,C,D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.
动点P从边长为1的正方形ABCD的顶点A出发顺次经过B,C,D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com