
分析 根据直线与双曲线相交的情形,分两种情况讨论:①AB只与双曲线右支相交,②AB与双曲线的两支都相交,分析其弦长的最小值,利用符合条件的直线的数目,综合可得答案.
解答 解:由题意,AB是通径时,|AB|=$\frac{8}{a}$=8,∴a=1
若AB只与双曲线右支相交时,|AB|的最小距离是通径,此时有两条直线符合条件,∴a>1;
若AB与双曲线的两支都相交时,此时|AB|的最小距离是实轴两顶点的距离,长度为2a=8,∴a=4,结合双曲线的对称性,此时有2条直线符合条件,a<4;
综合可得,有4条直线符合条件时,1<a<4;
故答案为1<a<4.
点评 本题考查直线与双曲线的关系,解题时可以结合双曲线的几何性质,分析直线与双曲线的相交的情况,分析其弦长最小值,从而求解;要避免由弦长公式进行计算.


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=$\frac{3}{2}$,b=-3 | B. | a=$\frac{2}{3}$,b=-3 | C. | a=$\frac{3}{2}$,b=3 | D. | a=$\frac{2}{3}$,b=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
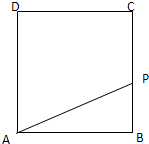 动点P从边长为1的正方形ABCD的顶点A出发顺次经过B,C,D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.
动点P从边长为1的正方形ABCD的顶点A出发顺次经过B,C,D再回到A,设x表示P点的行程,f(x)表示PA的长,g(x)表示△ABP的面积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4) | B. | (0,4] | C. | (0,2] | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | -$\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com