
ij���ʻ�ױƷ������ҵΪ��ռ�и�����г��ݶ����2016��������˻��ڼ����һϵ�д�����������г�����Ͳ��㣬��ױƷ�������� ������������
������������ ��Ԫ֮������
��Ԫ֮������ ��
�� �ɷ����������������������ױƷ��������ֻ����1�������֪2016��������ױƷ���豸�۾ɣ�ά�ȹ̶�����Ϊ3��Ԫ��ÿ����1�����ױƷ����Ͷ��32��Ԫ���������ã�����ÿ����ױƷ���ۼ۶�Ϊ�������ɱ���150%��ƽ��ÿ�������ѵ�һ��ĺͣ����������Ļ�ױƷ���������ꡣ
�ɷ����������������������ױƷ��������ֻ����1�������֪2016��������ױƷ���豸�۾ɣ�ά�ȹ̶�����Ϊ3��Ԫ��ÿ����1�����ױƷ����Ͷ��32��Ԫ���������ã�����ÿ����ױƷ���ۼ۶�Ϊ�������ɱ���150%��ƽ��ÿ�������ѵ�һ��ĺͣ����������Ļ�ױƷ���������ꡣ
��1�� ��2016������� (��Ԫ)��ʾΪ������
(��Ԫ)��ʾΪ������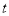 ��Ԫ�ĺ���.
��Ԫ�ĺ���.
��2�� ����ҵ2016��Ĵ�����Ͷ�����ʱ����ҵ�����������
(ע������=��������-�����ɱ�-�����ѣ������ɱ�=�̶�����+��������)

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015-2016ѧ�����˼����ѧ�߶�������������ѧ�Ծ��������棩 ���ͣ�ѡ����
���� ��
�� �ϵļ�ֵ���λ���У� ��
�ϵļ�ֵ���λ���У� ��
A��0�� B��1�� C��2�� D��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ������ʯ��ɽ���и߶��������Ŀ���ѧ�Ծ��������棩 ���ͣ�ѡ����
����p������y=log2��x2��2x���ĵ�����������[1��+�ޣ�������q������y= ��ֵ��Ϊ��0��1���������������������Ϊ�� ��
��ֵ��Ϊ��0��1���������������������Ϊ�� ��
A��p��q B��p��q C��p�ģ��Vq�� D���Vq
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ��ӱ���̨һ�и߶��������Ŀ���ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪����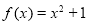 �Ķ�����Ϊ
�Ķ�����Ϊ ,ֵ��Ϊ[1,5],����ƽ��ֱ������ϵ��,��
,ֵ��Ϊ[1,5],����ƽ��ֱ������ϵ��,�� ���˶��켣����������Χ�ɵ�ͼ�ε�����ǣ� ��
���˶��켣����������Χ�ɵ�ͼ�ε�����ǣ� ��
A��8 B��6 C��4 D��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ��ӱ���̨һ�и߶��������Ŀ���ѧ�Ծ��������棩 ���ͣ�ѡ����
�輯�� ,����
,���� ����
Ϊ���� �Ķ�����,��
�Ķ�����,�� �� ��
�� ��
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ��㶫ʡ��һ��������ѧ�Ծ��������棩 ���ͣ������
��֪���� ��
�� ����|
����| |��1��|
|��1��| |��2��
|��2�� ��
�� �ļн�Ϊ120�㣮
�ļн�Ϊ120�㣮
��1�� �� ��
��
 ��
��
 ��
��
��2�������� ��
�� ��
�� ��
�� �ļн�Ϊ
�ļн�Ϊ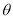 ����
���� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ��㶫ʡ��һ��������ѧ�Ծ��������棩 ���ͣ�ѡ����
�� ����
���� ����
���� Ϊ �� ��
Ϊ �� ��
A. B.
B. C.
C. D.
D. ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ������һ�и�һ��ѧ��������ѧ�Ծ��������棩 ���ͣ������
�� ����
���� ����
���� ����СֵΪ__________.
����СֵΪ__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�����������ѧ�߶�������������ѧ�Ծ��������棩 ���ͣ������
��֪������ ���ϵ���Բ
���ϵ���Բ ��������Ϊ
��������Ϊ ���ҹ���
���ҹ��� ��������Բ����Ķ�ֱ��
��������Բ����Ķ�ֱ�� ����Բ
����Բ ����
���� ��
�� ���㣬��
���㣬��
��1����Բ �ı����̣�
�ı����̣�
��2���������� ��������ֵ������ȡ����ֵʱֱ��
��������ֵ������ȡ����ֵʱֱ�� ��
�� ��б��֮��.
��б��֮��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com