练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，矩形ABCD和梯形BEFC所在平面互相垂直.，，，，，，.

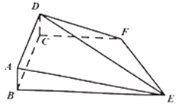
    （1）求证：平面ABE；

    （2）求二面角的余弦值.

    【答案】（1）证明见解析（2）

    【解析】

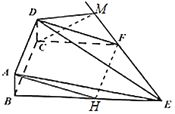
    （1）在BE上取点H，使得，可得四边形BCFH为矩形，得到，进一步得到，则四边形FDAH为平行四边形，故，由线面平行的判定可得平面ABE；

    （2）由平面平面BEFC结合面面垂直的性质可得平面BEFC，过C作交EF的延长线于M，连接DM，可得为二面角的平面角，然后求解三角形得答案.

    （1）证明：在BE上取点H，使得，则四边形BCFH为矩形，∴，

    又，∴，则四边形FDAH为平行四边形，故.

    ∵平面ABE，平面ABE，

    ∴平面ABE；

    （2）解：∵平面平面BEFC，平面平面，，

    ∴平面BEFC，

    过C作交EF的延长线于M，连接DM，

    则为二面角的平面角，

    在梯形BCEF中，由，，可得，

    ∴，

    又，∴，

    又，∴.

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知直三棱柱中，，，是的中点，是上一点，且.

    （Ⅰ）证明：平面；

    （Ⅱ）求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 (其中)，若点是函数图象的一个对称中心．

    (1)求的解析式，并求的最小正周期；

    (2)将函数的图象向左平移个单位，再将所得图象上各点的横坐标伸长为原来的倍，纵坐标不变，得到函数的图象，用 “五点作图法”作出函数在区间上的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，抛物线关于轴对称，它的顶点在坐标原点，点、、均在抛物线上.

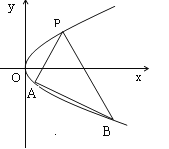
    （1）写出该抛物线的方程及其准线方程；

    （2）当与的斜率存在且倾斜角互补时，求的值及直线的斜率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义为不超过的最大整数，例如，．已知是等比数列，若，且前项和为．

    （1）若不等式对任意的恒成立，求实数的取值范围；

    （2）求的通项公式；

    （3）若，求数列的前项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线:（）上横坐标为4的点到焦点的距离为5．

    （1）求抛物线的方程；

    （2）设直线与抛物线交于不同两点，若满足，证明直线恒过定点，并求出定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国南宋数学家杨辉在所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律，现把杨辉三角中的数从上到下，从左到右依次排列，得数列：1，1，1，1，2，1，1，3，3，1，1，4，6，4，1，…，记作数列，若数列的前项和为，则_____．

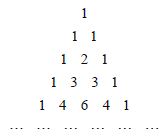
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为直角梯形，，，平面底面，为的中点，是棱上的点，，，．

    （1）求证：平面平面；

    （2）若，求二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f(α)＝

    (1)化简f(α)；

    (2)若α是第三象限角,且cos(α－)＝，求f(α)；

    (3)若α＝－1860°，求f(α)．

    查看答案和解析>>

    同步练习册答案