
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生,新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女生 | 40 | 40 |
(1)通过估算,试判断男、女哪种性别的学生愿意投入到新生接待工作的概率更大.
(2)能否有99%的把握认为,愿意参加新生接待工作与性别有关?
附: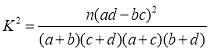 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() .
.
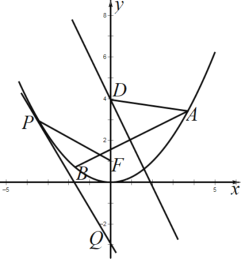
![]() 若点
若点![]() 为抛物线上异于原点的任一点,过点
为抛物线上异于原点的任一点,过点![]() 作抛物线的切线交
作抛物线的切线交![]() 轴于点
轴于点![]() ,证明:
,证明:![]() .
.
![]()
![]() ,
,![]() 是抛物线上两点,线段
是抛物线上两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() (
(![]() 不与
不与![]() 轴平行),且
轴平行),且![]() .过
.过![]() 轴上一点
轴上一点![]() 作直线
作直线![]() 轴,且
轴,且![]() 被以
被以![]() 为直径的圆截得的弦长为定值,求
为直径的圆截得的弦长为定值,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的两顶点分别为
的两顶点分别为![]() ,
,![]() 为双曲线的一个焦点,
为双曲线的一个焦点,![]() 为虚轴的一个端点,若在线段
为虚轴的一个端点,若在线段![]() 上(不含端点)存在两点
上(不含端点)存在两点![]() ,使得
,使得![]() ,则双曲线的渐近线斜率
,则双曲线的渐近线斜率![]() 的平方的取值范围是( )
的平方的取值范围是( )
A.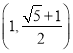 B.
B.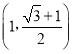 C.
C.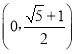 D.
D.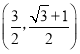
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an},等比数列{bn}满足:a1=b1=1,a2=b2,2a3-b3=1.
(1)求数列{an},{bn}的通项公式;
(2)记cn=anbn,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着时代的发展和社会的进步,“农村淘宝”发展十分迅速,促进“农产品进城”和“消费品下乡”.“农产品进城”很好地解决了农产品与市场的对接问题,使农民收入逐步提高,生活水平得到改善,农村从事网店经营的人收入逐步提高.西凤脐橙是四川省南充市的特产,因果实呈椭圆形、色泽橙红、果面光滑、无核、果肉脆嫩化渣、汁多味浓,深受人们的喜爱.为此小王开网店销售西凤脐橙,每月月初购进西凤脐橙,每售出1吨西凤脐橙获利润800元,未售出的西凤脐橙,每1吨亏损500元.经市场调研,根据以往的销售统计,得到一个月内西凤脐橙市场的需求量的频率分布直方图如图所示.小王为下一个月购进了100吨西凤脐橙,以x(单位:吨)表示下一个月内市场的需求量,y(单位:元)表示下一个月内经销西凤脐橙的销售利润.
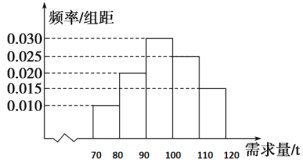
(1)将y表示为x的函数;
(2)根据频率分布直方图估计小王的网店下一个月销售利润y不少于67000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率,(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求小王的网店下一个月销售利润y的分布列和数学期望.
的频率),求小王的网店下一个月销售利润y的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 的底面
的底面![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]()
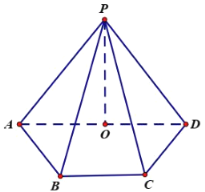
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() ?若存在指出点
?若存在指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com