
�躯��f(x)�Ķ�����ΪD�������ڷ���ʵ��lʹ�ö�������x��M(M⊆D)����x��l��D����f(x��l)��f(x)����ƺ���f(x)ΪM�ϵ�l�ߵ��������ָ����������⣺
�ٺ���f(x)��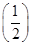 x��R�ϵ�1�ߵ�������
x��R�ϵ�1�ߵ�������
�ں���f(x)��sin 2xΪR�ϵĦиߵ�������
�����������Ϊ[��1������)�ĺ���f(x)��x2Ϊ[��1������)�ϵ�m�ߵ���������ôʵ��m��ȡֵ��Χ��[2������)��
������ȷ��������________��(д��������ȷ��������)

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�躯��f(x)��x2��1��������x��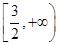 ��f
��f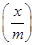 ��4m2f(x)��f(x��1)��4f(m)���������ʵ��m��ȡֵ��Χ��________��
��4m2f(x)��f(x��1)��4f(m)���������ʵ��m��ȡֵ��Χ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪f(x)��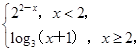 ���������x��R��af2(x)��f(x)��1��������ʵ��a����СֵΪ________��
���������x��R��af2(x)��f(x)��1��������ʵ��a����СֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
������y=f(x)(x��R)����f(x+2)=f(x),��x��[-1,1]ʱ,f(x)=1-x2,����g(x)=lg|x|,����y=f(x)��y=g(x)��ͼ��������[-5,5]�ڵĽ������Ϊ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����f(x)��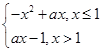 ��?x1��x2��R��x1��x2��ʹ��f(x1)��f(x2)��������ʵ��a��ȡֵ��Χ��________��
��?x1��x2��R��x1��x2��ʹ��f(x1)��f(x2)��������ʵ��a��ȡֵ��Χ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪[x]��ʾ������ʵ��x�������������[1.8]��1��[��1.2]����2.x0�Ǻ���f(x)��ln x��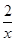 ����㣬��[x0]��________.
����㣬��[x0]��________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com