
【题目】如图(1),在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=![]() AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).
AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).
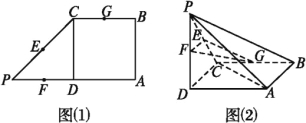
(1)求证:AP∥平面EFG;
(2)求三棱锥P-ABC的体积.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(I)利用三角形的中位线定理、平行线的传递性、平行四边形的判定定理、线面平行的判定定理等即可得出;(II)由已知点P在平面ABCD上的射影为点D,可得PD⊥平面ABCD.即PD是三棱锥P-ABC的高.利用三棱锥P-ABC的体积V=![]() S△ABC×PD即可得出
S△ABC×PD即可得出
试题解析:(I)证明:取AD的中点H,连接FH、GH.
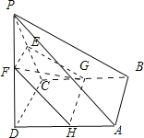
∵E,F,G分别为PC、PD、CB的中点,∴EF∥CD,CG![]() DH,
DH,
∴四边形CDHG是平行四边形,∴CD∥GH.
∴EF∥GH.∴四点EFHG四点共面.又FH∥PA.
PA平面EFGH,FH平面EFGH.∴PA∥平面EFGH.
(II)解:∵点P在平面ABCD上的射影为点D,∴PD⊥平面ABCD.
即PD是三棱锥P-ABC的高.
而![]() .
.
∴三棱锥P-ABC的体积V=![]() .
.


科目:高中数学 来源: 题型:
【题目】下列关于算法的叙述中正确的是( )
A. —个算法必须能解决一类问题 B. 求解某个问题的算法是唯一的
C. 算法不能重复使用 D. 算法的过程可以是无限的
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则![]() ;
;
②若C为双曲线,则![]() 或
或![]() ;
;
③曲线C不可能是圆;
④若![]() ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为![]() ;
;
⑤若![]() ,曲线C为双曲线,且虚半轴长为
,曲线C为双曲线,且虚半轴长为![]() .
.
其中真命题的序号为____________.(把所有正确命题的序号都填在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若洗水壶要用 1 分钟、烧开水要用 10 分钟、洗茶杯要用 2 分钟、取茶叶要用 1 分钟、 沏茶 1 分钟,那么较合理的安排至少也需要 ( )
A. 10分钟 B. 11分钟 C. 12分钟 D. 13分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①方程![]() 若有一个正实根,一个负实根,则
若有一个正实根,一个负实根,则![]() ;
;
②函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③函数![]() 的值域是
的值域是![]() ,则函数
,则函数![]() 的值域为
的值域为![]() ;
;
④一条曲线![]() 和直线
和直线![]() 的公共点个数是
的公共点个数是![]() ,则
,则![]() 的值不可能是1.
的值不可能是1.
其中正确的有 (写出所有正确的命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,圆![]() 的方程为
的方程为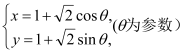 .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程
的极坐标方程![]() .
.
(Ⅰ)当![]() 时,判断直线
时,判断直线![]() 与
与![]() 的关系;
的关系;
(Ⅱ)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com