
分析 (1)利用乘法原理可求出基本事件的总数.利用一元二次方程有实数根(函数有零点)的充要条件即可得出所包括基本事件的个数;
(2)Ω对应的平面区域为10,计算函数y=f(x)在区间[1,+∞)上是增函数对应的平面区域的面积,代入几何概型概率计算公式,可得答案.
解答 解:(1)∵集合P={1,2,3},Q={-1,1,2,3,4},
分别从集合P和Q中随机取一个数作为a和b,(a,b)共有:
(1,-1),(1,1),(1,2),(1,3),(1,4),
(2,-1),(2,1),(2,2),(2,3),(2,4),
(3,-1),(3,1),(3,2),(3,3),(3,4)15种情况.
满足△=b2-4a≥0,有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共6种情况.
∴函数y=f(x)有零点的概率P=$\frac{6}{15}$=$\frac{2}{5}$.
(2)∵a是从区间[1,3]任取的一个数,b是从区间[-1,4]任取的一个数,
∴Ω=$\left\{(a,b)\right|\left\{\begin{array}{l}1≤a≤3\\-1≤b≤4\end{array}\right.\}$,
则Ω对应的平面区域为10,
计函数y=f(x)在区间[1,+∞)上是增函数为事件A,
则A=$\left\{(a,b)\right|\left\{\begin{array}{l}1≤a≤3\\-1≤b≤\\ \frac{b}{2a}≤1\end{array}\right.\}$,
A对应的平面区域如图中阴影部分所示: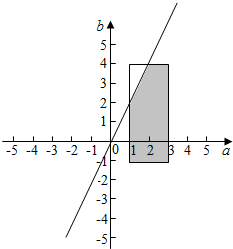
平面区域A的面积为:10-$\frac{1}{2}×2×1$=9,
故函数y=f(x)在区间[1,+∞)上是增函数的概率P=$\frac{9}{10}$
点评 掌握乘法原理、一元二次方程有实数根(函数有零点)的充要条件、二次函数的单调性、古典概型的计算公式是解题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,1] | B. | ($\frac{1}{2}$,+∞) | C. | (-∞,0)∪($\frac{1}{2}$,1] | D. | (-∞,0)∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com