
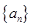 中,
中,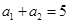 ,
,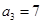 ,记数列
,记数列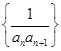 的前
的前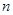 项和为
项和为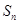 .
.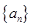 的通项公式;
的通项公式;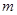 、
、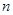 ,且
,且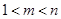 ,使得
,使得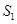 、
、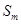 、
、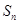 成等比数列?若存在,求出所有符合条件的
成等比数列?若存在,求出所有符合条件的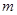 、
、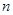 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.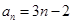 ;(2)存在,且
;(2)存在,且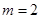 ,
, .
. 即可求出等差数列
即可求出等差数列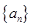 的通项公式;(2)先将数列
的通项公式;(2)先将数列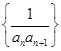 的通项公式结构选择裂项求和法求数列
的通项公式结构选择裂项求和法求数列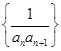 的前
的前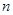 项和
项和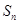 ,然后根据条件列式,利用正整数的一些相关性质列不等式求出
,然后根据条件列式,利用正整数的一些相关性质列不等式求出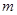 、
、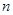 的值.
的值.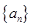 的公差为
的公差为 ,
,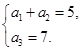 即
即 2分
2分 3分
3分 .
.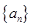 的通项公式为
的通项公式为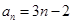
 . 4分
. 4分 , 5分
, 5分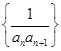 的前
的前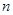 项和
项和

 . 7分
. 7分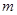 、
、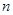 ,且
,且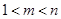 ,使得
,使得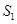 、
、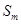 、
、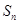 成等比数列,
成等比数列, . 8分
. 8分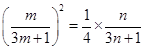 . 9分
. 9分 .
. ,所以
,所以 .
. .
. ,所以
,所以 .
.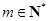 ,所以
,所以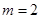 . 12分
. 12分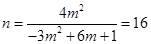 . 13分
. 13分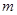 、
、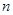 ,且只有一组解,即
,且只有一组解,即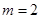 ,
, . 14分
. 14分

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com