
已知双曲线 的焦距为
的焦距为 ,其一条渐近线的倾斜角为
,其一条渐近线的倾斜角为 ,且
,且 ,以双曲线
,以双曲线 的实轴为长轴,虚轴为短轴的椭圆为
的实轴为长轴,虚轴为短轴的椭圆为 .
.
(1)求椭圆 的方程;
的方程;
(2)设点 是椭圆
是椭圆 的左顶点,
的左顶点,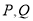 为椭圆
为椭圆 上异于点
上异于点 的两动点,若直线
的两动点,若直线 的斜率之积为
的斜率之积为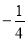 ,问直线
,问直线 是否恒过定点?若横过定点,求出该点坐标;若不横过定点,说明理由.
是否恒过定点?若横过定点,求出该点坐标;若不横过定点,说明理由.
科目:高中数学 来源:2016届湖南师范大学附中高三上学期月考三文科数学试卷(解析版) 题型:选择题
已知平面上不重合的四点 满足
满足 ,且
,且 ,那么实数
,那么实数 的值为( )
的值为( )
A.2 B. C.4 D.5
C.4 D.5
查看答案和解析>>
科目:高中数学 来源:2016届山东省高三11月月考数学试卷(解析版) 题型:解答题
设关于 的函数
的函数 ,其中
,其中 为实数集R上的常数,函数
为实数集R上的常数,函数 在
在 处取得极值0.
处取得极值0.
(1)已知函数 的图象与直线
的图象与直线 有两个不同的公共点,求实数k的取值范围;
有两个不同的公共点,求实数k的取值范围;
(2)设函数 , 其中
, 其中 ,若对任意的
,若对任意的 ,总有
,总有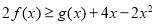 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届辽宁省抚顺市高三12月月考文科数学试卷(解析版) 题型:解答题
为了调查学生星期天晚上学习时间利用问题,某校从高二年级1000名学生(其中走读生450名,住宿生550名)中,采用分层抽样的方法抽取 名学生进行问卷调查,根据问卷取得了这
名学生进行问卷调查,根据问卷取得了这 名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组①
名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组① ,②
,②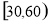 ,③
,③ ,④
,④ ,⑤
,⑤ ,⑥
,⑥ ,⑦
,⑦ ,⑧
,⑧ ,得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:
,得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:
(1)求 的值并补全下列频率分布直方图;
的值并补全下列频率分布直方图;
(2)如果把“学生晚上学习时间达到两小时”作为是否充分利用时间的标准,对抽取的 名学生,完成下列
名学生,完成下列 列联表:
列联表:
利用时间充分 | 利用时间不充分 | 总计 | |
走读生 | |||
住宿生 | 10 | ||
总计 |
据此资料,你是否认为学生“利用时间是否充分”与走读、住宿有关?
参考公式:

查看答案和解析>>
科目:高中数学 来源:2016届湖南师大附中高三月考四文科数学试卷(解析版) 题型:解答题
选修4—4:坐标系与参数方程
已知曲线 的极坐标方程式
的极坐标方程式 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 ,(
,( 为参数).
为参数).
(1)求曲线 的直角坐标方程和直线
的直角坐标方程和直线 的普通方程;
的普通方程;
(2)设点 ,若直线
,若直线 与曲线
与曲线 交于两点
交于两点 ,且
,且 ,求实数
,求实数 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2016届湖南省长沙市高三第一次月考文科数学试卷(解析版) 题型:解答题
今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
(1)求上表中的 、
、 的值,并补全下图所示的频率分布直方图;
的值,并补全下图所示的频率分布直方图;

(2)在被调查的居民中,若从年龄在 ,
, 的居民中各随机选取1人参加消防知识讲座,求选中的两人中仅有一人不知道灭火器的使用方法的概率.
的居民中各随机选取1人参加消防知识讲座,求选中的两人中仅有一人不知道灭火器的使用方法的概率.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省吉安市高二上期中理科数学试卷(解析版) 题型:解答题
如图,四棱锥 中,底面ABCD为菱形,且
中,底面ABCD为菱形,且 ,
, .
.

(1)求证: ;
;
(2)若 ,求点C到平面PBD的距离.
,求点C到平面PBD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com