
分析 利用新定义,求出函数解析式,再求导数,确定切线的斜率,即可得出结论.
解答 解:由题意,f(x)=$\frac{1}{3}{x}^{3}-\frac{1}{3}{x}^{2}-x$,
∴f′(x)=${x}^{2}-\frac{2}{3}x-1$,
∴f′(1)=-$\frac{2}{3}$,
∵f(1)=-1,
∴函数f(x)=$(\begin{array}{l}{{x}^{2}-x}&{1}\\{x}&{\frac{x}{3}}\end{array})$的图象在点(1,-1)处的切线方程是2x+3y+1=0,
故答案为2x+3y+1=0.
点评 本题考查导数的几何意义,新定义的应用,考查学生的计算能力,确定函数的解析式是关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
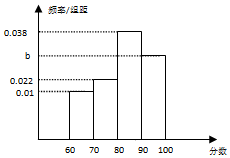 某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题:
某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题:| 分组 | 频数 | 频率 |
| [60,70) | 10 | 0.1 |
| [70,80) | 22 | 0.22 |
| [80,90) | a | 0.38 |
| [90,100] | 30 | c |
| 合计 | 100 | d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | 5 | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com