
分析 (1)已知通项公式变形,利用等比数列的性质判断得证,求出数列{an}的通项公式即可;
(2)根据题意表示出数列{n•an-n}的前n项和Sn,利用数列的递推式确定出Sn通项公式即可.
解答 证明:(1)由an=2an-1-1,得an-1=2(an-1-1),
∴数列{an-1}构成首项为a1-1=1,公比q=2的等比数列,
∴an-1=2n-1,即an=2n-1+1;
解:(2)∵nan-n=n•2n-1+n-n=n•2n-1,
∴Sn=1•20+2•21+3•22+…+n•2n-1,①,
2Sn=1•21+2•22+3•23+…+n•2n,②,
②-①,得:Sn=-20-21-22-…-2n-1+n•2n=-$\frac{1-{2}^{n}}{1-2}$+n•2n=n•2n+1-2n=(n-1)2n+1.
点评 此题考查了数列的求和,以及等比数列的通项公式,熟练掌握等比数列的通项公式是解本题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | m-y>n-x | B. | xm>yn | C. | $\frac{x}{n}>\frac{y}{m}$ | D. | x-m>y-n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{4}]$ | B. | $(-∞,\frac{1}{4})$ | C. | (-2,0) | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
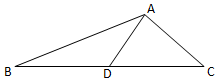 △ABC中,角A,B,C的对边分别为a,b,c,A=$\frac{3π}{4}$,sinB=$\frac{\sqrt{10}}{10}$,D为BC边中点,AD=1.
△ABC中,角A,B,C的对边分别为a,b,c,A=$\frac{3π}{4}$,sinB=$\frac{\sqrt{10}}{10}$,D为BC边中点,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com