
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
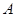
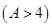 立方米时,只付基本费3元+每户每月定额保险费
立方米时,只付基本费3元+每户每月定额保险费
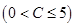 元;若用气量超过
元;若用气量超过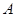 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付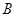 元.
元.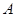 、
、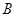 、
、 的值;
的值; 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题
 m,盖子边长为
m,盖子边长为 m,
m,
 关于
关于 的解析式;
的解析式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。 时,求函数V(x)的表达式;
时,求函数V(x)的表达式; 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
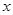 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为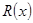 万元,且
万元,且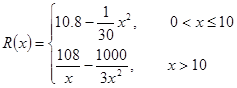 .
.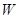 (万元)关于年产量
(万元)关于年产量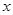 (千件)的函数解析式;
(千件)的函数解析式; 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的图象上, 那么称[A, B]为函数f(x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数
的图象上, 那么称[A, B]为函数f(x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数 关于原点的中心对称点的组数为_____________
关于原点的中心对称点的组数为_____________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com