
【题目】已知函数![]() ,其图象的一条切线为
,其图象的一条切线为![]() .
.
(1)求实数![]() 的值;
的值;
(2)求证:若![]() ,则
,则![]() .
.
【答案】(1)![]() ;(2)答案见解析
;(2)答案见解析
【解析】
(1)假设切点,根据曲线在某点处导数的几何意义,以及已知的切线方程,可得![]() ,然后研究
,然后研究![]() 可得
可得![]() ,最后代值计算,可得结果.
,最后代值计算,可得结果.
(2)构建函数![]() ,计算
,计算![]() ,并利用二阶导判断
,并利用二阶导判断![]() 的单调性,根据
的单调性,根据![]() 的值域来判断
的值域来判断![]() 的单调性,进一步求得
的单调性,进一步求得![]() ,可得结果.
,可得结果.
(1)函数定义域为![]()
∵![]() ,∴
,∴![]() .
.
由题可知:
![]() 在点
在点![]() 处的切线为
处的切线为![]() ,
,
则![]() 且
且![]() ,
,
∴![]() ,即
,即![]() .
.
令![]() ,
,
则![]() .
.
当![]() 时,
时,
![]() ,
,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,
![]() ,
,![]() 在
在![]() 单调递减.
单调递减.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
∴![]() ,
,![]() .故实数
.故实数![]() 的值为
的值为![]() .
.
(2)令![]()
即![]()
则![]() .
.
即![]()
令![]() ,
,
则![]() ,
,
∵![]() 恒成立,
恒成立,
∴![]() 在
在![]() 单调递减,即
单调递减,即![]() 在
在![]() 单调递减.
单调递减.
又![]() ,
,
![]() ,
,
∴![]() ,使得
,使得![]() .
.
∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
∴![]() .
.
又![]() ,即
,即![]() ,
,
∴![]() ,
,
![]()
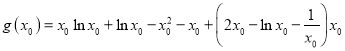
![]() .
.
令![]() ,
,![]() .
.
则![]() .
.
∵![]() 恒成立,
恒成立,
∴![]() ,故
,故![]() 在
在![]() 单调递增.
单调递增.
∴![]() ,
,
故![]() ,
,
即![]() .
.
∴当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,设抛物线![]() 的焦点为F,准线为l,过准线l上一点
的焦点为F,准线为l,过准线l上一点![]() 且斜率为k的直线
且斜率为k的直线![]() 交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.
交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.
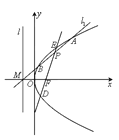
(1)求抛物线C的方程及k的取值范围;
(2)是否存在k值,使点P是线段DE的中点?若存在,求出k值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个统计案例如下:
①为了探究患慢性支气管炎与吸烟关系,调查了339名50岁以上的人,调查结果如表:
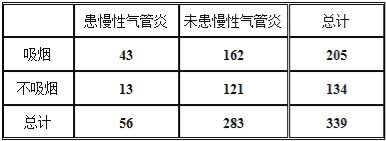
②为了解某地母亲与女儿身高的关系,随机测得10对母女的身高如下表: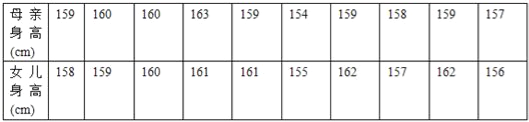
则对这些数据的处理所应用的统计方法是( )
A.①回归分析②取平均值
B.①独立性检验②回归分析
C.①回归分析②独立性检验
D.①独立性检验②取平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
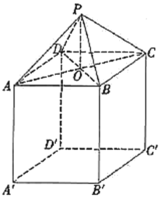
【题目】如图所示,一个仓库设计由上部屋顶和下部主体两部分组成,屋顶的形状是四棱锥![]() ,四边形
,四边形![]() 是正方形,点
是正方形,点![]() 为正方形
为正方形![]() 的中心,
的中心,![]() 平面
平面![]() ;下部的形状是长方体
;下部的形状是长方体![]() .已知上部屋顶造价与屋顶面积成正比,比例系数为
.已知上部屋顶造价与屋顶面积成正比,比例系数为![]() ,下部主体造价与高度成正比,比例系数为
,下部主体造价与高度成正比,比例系数为![]() .若欲造一个上、下总高度为10
.若欲造一个上、下总高度为10![]() ,
,![]()
![]() 的仓库,则当总造价最低时,
的仓库,则当总造价最低时,![]() ( )
( )
A.![]()
![]() B.
B.![]()
![]() C.4
C.4![]() D.
D.![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障人民群众的身体健康,在预防新型冠状病毒期间,贵阳市市场监督管理局加强了对市场的监管力度,对生产口罩的某工厂利用随机数表对生产的![]() 个口罩进行抽样测试是否合格,先将
个口罩进行抽样测试是否合格,先将![]() 个口罩进行编号,编号分别为
个口罩进行编号,编号分别为![]() ;从中抽取
;从中抽取![]() 个样本,如下提供随机数表的第
个样本,如下提供随机数表的第![]() 行到第
行到第![]() 行:
行:
![]()
![]()
![]()
若从表中第![]() 行第
行第![]() 列开始向右依次读取
列开始向右依次读取![]() 个数据,则得到的第
个数据,则得到的第![]() 个样本编号为( )
个样本编号为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三角形的边长为不相等的整数,且最大边长为n,这些三角形的个数为an.
(1)求数列{an}的通项公式;
(2)在1,2,…,100中任取三个不同的整数,求它们可以是一个三角形的三条边长的概率.
附:1+22+32+…+n2![]() ;1+23+33+…+n3
;1+23+33+…+n3![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数,且
为常数,且![]() .
.
(1)若![]() 是奇函数,求
是奇函数,求![]() 的取值集合
的取值集合![]() ;
;
(2)当![]() 时,设
时,设![]() 的反函数
的反函数![]() ,且
,且![]() 的图象与
的图象与![]() 的图象关于
的图象关于![]() 对称,求
对称,求![]() 的取值集合
的取值集合![]() ;
;
(3)对于问题(1)(2)中的![]() 、
、![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com