
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点且
两点且![]() .求证:
.求证: ![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台问政直播节目首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A部门 | 50% | 25% | 25% |
B部门 | 80% | 0 | 20% |
C部门 | 50% | 50% | 0 |
D部门 | 40% | 20% | 40% |

(1)若市民甲选择的是A部门,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的市民中再选出2人进行电视访谈,求这两人中至少有一人选择的是D部门的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M在椭圆![]()
![]() 上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
(Ⅰ)若圆M与y轴相切,求椭圆的离心率;
(Ⅱ)若圆M与y轴相交于A,B两点,且![]() 是边长为2的正三角形,求椭圆的方程.
是边长为2的正三角形,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 满足:
满足:![]() ,
,![]() .
.![]() 的前n项和为
的前n项和为![]() .
.
(Ⅰ)求![]() 及
及![]() ;
;
(Ⅱ)若![]() ,
,![]() (
(![]() ),求数列
),求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]() =
=![]()
【解析】
试题分析:(Ⅰ)设出首项a1和公差d ,利用等差数列通项公式,就可求出![]() ,再利用等差数列前项求和公式就可求出
,再利用等差数列前项求和公式就可求出![]() ;(Ⅱ)由(Ⅰ)知
;(Ⅱ)由(Ⅰ)知![]() ,再利用
,再利用![]() ,
,![]() (
(![]() ),就可求出
),就可求出![]() ,再利用错位相减法就可求出
,再利用错位相减法就可求出![]() .
.
试题解析:(Ⅰ)设等差数列{an}的首项为a1,公差为d
∵ ![]() ,
,![]() ∴
∴ ![]() 解得
解得 ![]()
∴ ![]()
![]() ,
,
(Ⅱ)∵ ![]() ,
,![]() ∴
∴ ![]()
∵![]() ∴
∴ ![]()
∴ ![]()
![]()
![]()
= ![]() (1-
(1- ![]() +
+ ![]() -
- ![]() +…+
+…+![]() -
-![]() )
)
=![]() (1-
(1-![]() ) =
) =![]()
所以数列![]() 的前
的前![]() 项和
项和![]() =
=![]() .
.
考点:1.等差数列的通项公式; 2. 等差数列的前n项和公式; 3.裂项法求数列的前n项和公式
【题型】解答题
【结束】
18
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
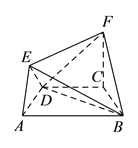
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在线段
)在线段![]() (含端点)上,是否存在一点
(含端点)上,是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法中:
①有两个面平行,其余各面都是平行四边形的几何体叫棱柱
②相等的线段在直观图中仍然相等
③一个直角三角形绕其一边旋转一周所形成的封闭图形叫圆锥
④用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查, 饮食指数结果用茎叶图表示如图, 图中饮食指数低于70的人是饮食以蔬菜为主;饮食指数高于70的人是饮食以肉类为主.

(1)完成下列2×2列联表:

能否有99%的把握认为老师的饮食习惯与年龄有关?
(2)从群力校区任选一名老师, 设“选到45岁以上老师”为事件![]() , “饮食指数高于70的老师”为事件
, “饮食指数高于70的老师”为事件![]() , 用调查的结果估计
, 用调查的结果估计![]() 及
及![]() (用最简分数作答);
(用最简分数作答);
(3)为了给食堂提供老师的饮食信息, 根据(1)(2)的结论,能否有更好的抽样方法来估计老师的饮食习惯, 并说明理由.附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com