
【题目】已知点M在椭圆![]()
![]() 上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
(Ⅰ)若圆M与y轴相切,求椭圆的离心率;
(Ⅱ)若圆M与y轴相交于A,B两点,且![]() 是边长为2的正三角形,求椭圆的方程.
是边长为2的正三角形,求椭圆的方程.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了鼓励节约用电,辽宁省实行阶梯电价制度,其中每户的用电单价与户年用电量的关系如下表所示.
分档 | 户年用电量(度) | 用电单价(元/度) |
第一阶梯 |
| 0.5 |
第二阶梯 |
| 0.55 |
第三阶梯 |
| 0.80 |
记用户年用电量为![]() 度时应缴纳的电费为
度时应缴纳的电费为![]() 元.
元.
(1)写出![]() 的解析式;
的解析式;
(2)假设居住在沈阳的范伟一家2018年共用电3000度,则范伟一家2018年应缴纳电费多少元?
(3)居住在大连的张莉一家在2018年共缴纳电费1942元,则张莉一家在2018年用了多少度电?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月31日晚上月全食的过程分为初亏、食既、食甚、生光、复圆五个阶段,月食的初亏发生在19时48分,20时51分食既,食甚时刻为21时31分,22时08分生光,直至23时12分复圆.全食伴随有蓝月亮和红月亮,全食阶段的“红月亮”将在食甚时刻开始,生光时刻结東,一市民准备在19:55至21:56之间的某个时刻欣赏月全食,则他等待“红月亮”的时间不超过30分钟的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,求弦长
两点,求弦长![]() ,若点
,若点![]() ,求
,求![]() 的值;
的值;
(2)以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 和圆
和圆![]() 的交点为
的交点为![]() ,
,![]() ,求弦
,求弦![]() 所在直线的直角坐标方程.
所在直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明在某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前54单没有奖励,超过54单的部分每单奖励20元.
(1)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
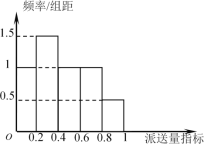
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在![]() 时,日平均派送量为
时,日平均派送量为![]() 单.若将频率视为概率,回答下列问题:
单.若将频率视为概率,回答下列问题:
①估计这100天中的派送量指标的平均数(同一组中的数据用该组区间的中点值作代表) ;
②根据以上数据,设每名派送员的日薪为![]() (单位:元),试分别求出甲、乙两种方案的日薪
(单位:元),试分别求出甲、乙两种方案的日薪![]() 的分布列及数学期望. 请利用数学期望帮助小明分析他选择哪种薪酬方案比较合适?并说明你的理由.
的分布列及数学期望. 请利用数学期望帮助小明分析他选择哪种薪酬方案比较合适?并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com