
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,求弦长
两点,求弦长![]() ,若点
,若点![]() ,求
,求![]() 的值;
的值;
(2)以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 和圆
和圆![]() 的交点为
的交点为![]() ,
,![]() ,求弦
,求弦![]() 所在直线的直角坐标方程.
所在直线的直角坐标方程.
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 上的动点,且
上的动点,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
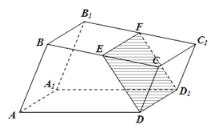
(1)证明:无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)当![]() 时,求几何体
时,求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学理科成绩优异,今年参加了数学,物理,化学,生物4门学科竞赛.已知该同学数学获一等奖的概率为![]() ,物理,化学,生物获一等奖的概率都是
,物理,化学,生物获一等奖的概率都是![]() ,且四门学科是否获一等奖相互独立.
,且四门学科是否获一等奖相互独立.
(1)求该同学至多有一门学科获得一等奖的概率;
(2)用随机变量![]() 表示该同学获得一等奖的总数,求
表示该同学获得一等奖的总数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台问政直播节目首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A部门 | 50% | 25% | 25% |
B部门 | 80% | 0 | 20% |
C部门 | 50% | 50% | 0 |
D部门 | 40% | 20% | 40% |

(1)若市民甲选择的是A部门,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的市民中再选出2人进行电视访谈,求这两人中至少有一人选择的是D部门的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() ),圆
),圆![]() (
(![]() ),若圆
),若圆![]() 的一条切线
的一条切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)当![]() ,
, ![]() 时,若点
时,若点![]() 都在坐标轴的正半轴上,求椭圆
都在坐标轴的正半轴上,求椭圆![]() 的方程;
的方程;
(2)若以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,探究
,探究![]() 是否满足
是否满足![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M在椭圆![]()
![]() 上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
(Ⅰ)若圆M与y轴相切,求椭圆的离心率;
(Ⅱ)若圆M与y轴相交于A,B两点,且![]() 是边长为2的正三角形,求椭圆的方程.
是边长为2的正三角形,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 满足:
满足:![]() ,
,![]() .
.![]() 的前n项和为
的前n项和为![]() .
.
(Ⅰ)求![]() 及
及![]() ;
;
(Ⅱ)若![]() ,
,![]() (
(![]() ),求数列
),求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]() =
=![]()
【解析】
试题分析:(Ⅰ)设出首项a1和公差d ,利用等差数列通项公式,就可求出![]() ,再利用等差数列前项求和公式就可求出
,再利用等差数列前项求和公式就可求出![]() ;(Ⅱ)由(Ⅰ)知
;(Ⅱ)由(Ⅰ)知![]() ,再利用
,再利用![]() ,
,![]() (
(![]() ),就可求出
),就可求出![]() ,再利用错位相减法就可求出
,再利用错位相减法就可求出![]() .
.
试题解析:(Ⅰ)设等差数列{an}的首项为a1,公差为d
∵ ![]() ,
,![]() ∴
∴ ![]() 解得
解得 ![]()
∴ ![]()
![]() ,
,
(Ⅱ)∵ ![]() ,
,![]() ∴
∴ ![]()
∵![]() ∴
∴ ![]()
∴ ![]()
![]()
![]()
= ![]() (1-
(1- ![]() +
+ ![]() -
- ![]() +…+
+…+![]() -
-![]() )
)
=![]() (1-
(1-![]() ) =
) =![]()
所以数列![]() 的前
的前![]() 项和
项和![]() =
=![]() .
.
考点:1.等差数列的通项公式; 2. 等差数列的前n项和公式; 3.裂项法求数列的前n项和公式
【题型】解答题
【结束】
18
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
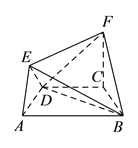
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在线段
)在线段![]() (含端点)上,是否存在一点
(含端点)上,是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com