某班有6位学生与班主任老师毕业前夕留影.要求班主任站在正中间且女生甲.乙不相邻.则排法的种数为( )A．96B．432C．480D．528 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

20．某班有6位学生与班主任老师毕业前夕留影，要求班主任站在正中间且女生甲、乙不相邻，则排法的种数为（　　）

A．

B．

432

C．

480

D．

528

分析利用间接法，求出班主任站在正中间的所有情况；班主任站在正中间且女生甲、乙相邻的情况，即可得出结论．

解答解：班主任站在正中间，有A₆⁶=720种；
班主任站在正中间且女生甲、乙相邻，有4A₂²A₄⁴=192种；
∴班主任站在正中间且女生甲、乙不相邻，排法的种数为720-192=528种．
故选：D．

点评本题考查计数原理的运用，考查排列知识，考查学生分析解决问题的能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

10．

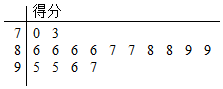某校就开展“学习习惯养成”教育活动的情况进行调查，随机抽取了16名学生进行测试，用“10分制”以茎叶图方式记录了他们的测试分数（如图），若所得分数不低于9.5分，则称该学生“学习习惯非常好”．
（1）现从这16人中随机选取3人，求至少有1人“学习习惯非常好”的概率；
（2）以这16人的样本数据估计该所学校学生的总体数据，若从该学校（人数很多）任选3人，记X表示抽到“学习习惯非常好”的人数，求X的分布列及数学期望EX．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

11．设cos（α-$\frac{π}{6}$）=$\frac{15}{17}$，α∈（$\frac{π}{6}$，$\frac{π}{2}$），则cosα的值为$\frac{{15\sqrt{3}-8}}{34}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．

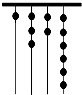远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，如图所示的是一位母亲记录的孩子自出生后的天数，在从右向左依次排列的不同绳子上打结，满七进一，根据图示可知，孩子已经出生的天数是（　　）

A．

336

B．

510

C．

1326

D．

3603

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．调查某医院某段时间内婴儿出生的时间与性别的关系，得到下面的数据：出生时间在晚上的男婴为24人，女婴为8人；出生时间在白天的男婴为31人，女婴为26人．
（1）将下面的2×2列联表补充完整；

出生时间性别	晚上	白天	合计
男婴
女婴
合计

（2）能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系？

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

5．已知α∈（-$\frac{π}{4}$，0），β∈（$\frac{π}{2}$，π），cos（α+β）=-$\frac{4}{5}$，cos（β-$\frac{π}{4}$）=$\frac{5}{13}$，则cos（α+$\frac{π}{4}$）=$\frac{16}{65}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．机动车驾驶证考试分理论考试和实际操作考试两部分进行，每部分考试成绩只记“合格”与“不合格”，两部分都“合格”者，则机动车驾驶证考试“合格”（并颁发机动车驾驶证）．甲、乙、丙三人在理论考试中“合格”的概率依次为$\frac{4}{5}$，$\frac{3}{4}$，$\frac{2}{3}$，在实际操作中“合格”的概率依次为$\frac{1}{2}$，$\frac{2}{3}$，$\frac{5}{6}$，所有考试是否合格相互之间没有影响．
（1）求这3人进行理论与实际操作两项考试后，恰有2人获得（机动车驾驶证）的概率；
（2）用X表示甲、乙、丙三人在理论考试中合格的人数，求X的分布列和数学期望E（X）．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．由1，2，3，4可组成54个三位数．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

10．已知数列{a_n}是等比数列，其中a₃=2，a₆=16，则该数列的公比q等于（　　）

A．

$\frac{14}{3}$

B．

C．

D．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学