
| A. | 16 | B. | 32 | C. | 4 | D. | 8 |
分析 由等比数列的性质结合已知得到${b}_{1}{b}_{2}…{b}_{8}={2}^{4}=16$,代入bn=$\frac{{{a_{n+1}}}}{a_n}$得到$\frac{{a}_{9}}{{a}_{1}}$=16.从而求得答案.
解答 解:∵数列{bn}为等比数列,
∴b1b8=b2b7=b3b6=b4b5=2,
∴${b}_{1}{b}_{2}…{b}_{8}={2}^{4}=16$.
则$\frac{{a}_{2}}{{a}_{1}}•\frac{{a}_{3}}{{a}_{2}}…\frac{{a}_{9}}{{a}_{8}}$=16.
∴a9=16a1=16.
故选:A.
点评 本题考查了数列递推式,考查了等比数列的性质,训练了累积法求数列的通项,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
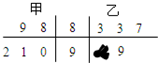 如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩不低于乙的平均成绩的概率为$\frac{9}{10}$.
如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩不低于乙的平均成绩的概率为$\frac{9}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com