
 辟为水果园,其中
辟为水果园,其中 ,
,  ,
, .若经过
.若经过 上一点
上一点 和
和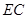 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 将四边形
将四边形 分成面积相等的两部分,设
分成面积相等的两部分,设 .
.
 的关系式;
的关系式; 是灌溉水管的位置,为了省钱,希望它最短,求
是灌溉水管的位置,为了省钱,希望它最短,求 的长的最小值;
的长的最小值; 是参观路线,希望它最长,那么
是参观路线,希望它最长,那么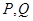 的位置在哪里?
的位置在哪里?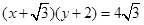 ;(2)
;(2)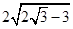 ;(3)P点在B处,Q点在E处.
;(3)P点在B处,Q点在E处.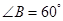 ,延长BD、CE交于点A,则由得出结论
,延长BD、CE交于点A,则由得出结论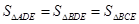 ,于是可知
,于是可知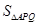 的面积,而它的面积又可用
的面积,而它的面积又可用 表示出来,于是问题得到解决;(2)
表示出来,于是问题得到解决;(2)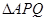 中利用余弦定理,可将
中利用余弦定理,可将 的长度用
的长度用 表示,再利用(1)的结果消去
表示,再利用(1)的结果消去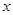 ,则得到
,则得到 关于
关于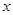 的函数关系式,然后利用基本不等式或求函数最值的一般方法求出函数的最小值或最大值,要注意函数的定义域;(3)思路同(2).
的函数关系式,然后利用基本不等式或求函数最值的一般方法求出函数的最小值或最大值,要注意函数的定义域;(3)思路同(2).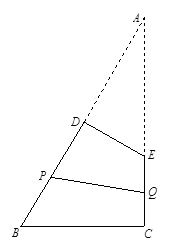
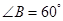 ,延长BD、CE交于点A,则
,延长BD、CE交于点A,则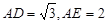 ,则
,则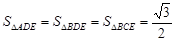 .
.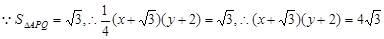 . 4分
. 4分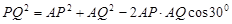
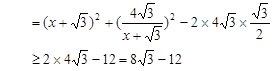 6分
6分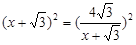 ,即
,即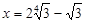 时,
时,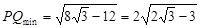 . 8分
. 8分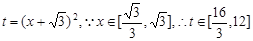 , 10分
, 10分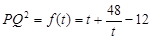 ,
,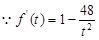 ,令
,令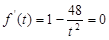 得,
得,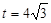 , 12分
, 12分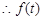 在
在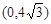 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,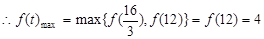 ,PQmax = 2, 14分
,PQmax = 2, 14分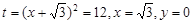 ,P点在B处,Q点在E处. 16分
,P点在B处,Q点在E处. 16分

科目:高中数学 来源:不详 题型:解答题
 与服药后的时间
与服药后的时间 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中 是线段,曲线段
是线段,曲线段 是函数
是函数
 是常数
是常数 的图象.
的图象.
 关于时间
关于时间 的函数关系式;
的函数关系式; 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?
 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少 ?
?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。 时,求函数V(x)的表达式;
时,求函数V(x)的表达式; 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
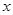 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为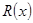 万元,且
万元,且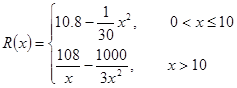 .
.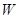 (万元)关于年产量
(万元)关于年产量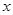 (千件)的函数解析式;
(千件)的函数解析式; 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的等域区间是 .
的等域区间是 .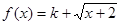 是布林函数,则实数k的取值范围是 .
是布林函数,则实数k的取值范围是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com