
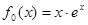 ,
,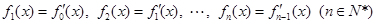 .
.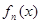 的表达式(不需证明);
的表达式(不需证明);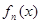 的极小值;
的极小值;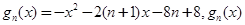 的最大值为
的最大值为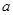 ,
,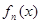 的最小值为
的最小值为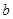 ,求
,求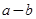 的最小值.
的最小值.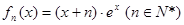 ;(2)
;(2)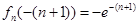 ;(3)
;(3)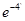 .
.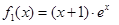 ,
,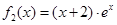 ,
,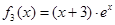 ,
,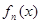 的表达式
的表达式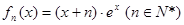 .
.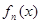 的极小值,先求出
的极小值,先求出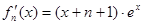 ,
,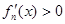 ,
,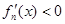 可得
可得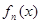 的单调区间和极值.
的单调区间和极值.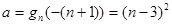 .
.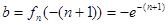 ,所以
,所以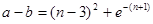 .
.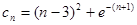 的最小值.这又有两种方法:
的最小值.这又有两种方法: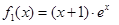 ,
,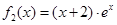 ,
,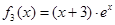 ,
,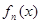 的表达式
的表达式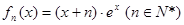 . 4分
. 4分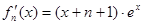 ,
,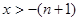 时,
时,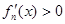 ;当
;当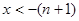 时,
时,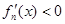 .
.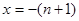 时,
时,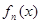 取得极小值
取得极小值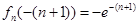 ,
,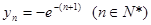 . 8分
. 8分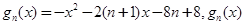 配方得
配方得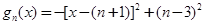 ,
,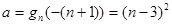 .
.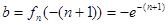 ,所以
,所以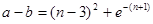 ,10分
,10分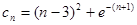 的最小值.
的最小值.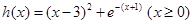 ,
,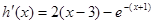 ,又
,又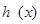 在区间
在区间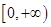 上单调递增,
上单调递增,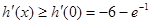 .
.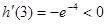 ,
,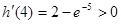 ,
,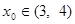 使得
使得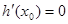 .
.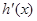 在区间
在区间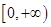 上单调递增,所以
上单调递增,所以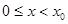 时,
时,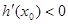 ;
;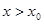 时,
时,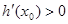 ,
,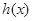 在区间
在区间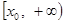 上单调递增,在区间
上单调递增,在区间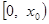 上单调递减,
上单调递减,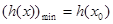 .
.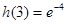 ,
,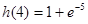 ,
,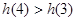 ,
,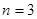 时,
时, 取得最小值
取得最小值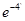 .
.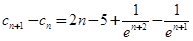 ,
,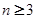 时,
时,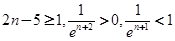 ,
, ,所以
,所以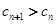 .
.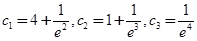 ,
,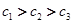 .
.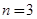 时,
时,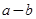 取得最小值
取得最小值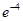 .14分
.14分

科目:高中数学 来源:不详 题型:解答题
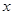 (元)与年产量
(元)与年产量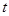 (吨)满足函数关系
(吨)满足函数关系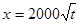 .若工厂每生产一吨产品必须赔付农场
.若工厂每生产一吨产品必须赔付农场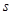 元(以下称
元(以下称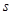 为赔付价格).
为赔付价格).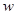 (元)表示为年产量
(元)表示为年产量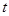 (吨)的函数,并求出工厂获得最大利润的年产量;
(吨)的函数,并求出工厂获得最大利润的年产量;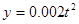 (元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格
(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格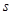 是多少?
是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 辟为水果园,其中
辟为水果园,其中 ,
,  ,
, .若经过
.若经过 上一点
上一点 和
和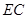 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 将四边形
将四边形 分成面积相等的两部分,设
分成面积相等的两部分,设 .
.
 的关系式;
的关系式; 是灌溉水管的位置,为了省钱,希望它最短,求
是灌溉水管的位置,为了省钱,希望它最短,求 的长的最小值;
的长的最小值; 是参观路线,希望它最长,那么
是参观路线,希望它最长,那么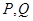 的位置在哪里?
的位置在哪里?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
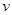 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度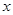 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到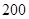 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当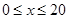 时,车流速度为
时,车流速度为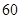 千米/小时.研究表明:当
千米/小时.研究表明:当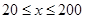 时,车流速度
时,车流速度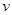 是车流密度
是车流密度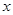 的一次函数.
的一次函数.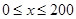 时,求函数
时,求函数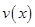 的表达式;
的表达式;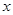 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)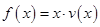 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
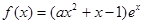 ,其中
,其中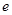 是自然对数的底数,
是自然对数的底数,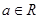 .
.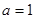 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;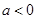 ,求
,求 的单调区间;
的单调区间; ,函数
,函数 的图象与函数
的图象与函数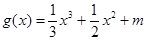 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数 的取值范围.
的取值范围. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 与
与 互为反函数,其图象关于直线
互为反函数,其图象关于直线 对称;
对称;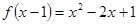 ,则
,则 ;
; 且
且 时,函数
时,函数 必过定点(2,-2);
必过定点(2,-2); 的值域是(0,+
的值域是(0,+ );
);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com