
(本小题满分13分)设F1,F2分别是椭圆 的左右焦点.
的左右焦点.
(1)若P是该椭圆上的一个动点,求 的最大值和最小值.
的最大值和最小值.
(2)是否存在经过点A(5,0)的直线l与椭圆交于不同的两点C,D,使得|F2C|=|F2D|?若存在,求直线l的方程;若不存在,请说明理由.
(1)最小值3,最大值4;(2)不存在
【解析】
试题分析:(1)将数量积转化为坐标表示,利用坐标的有界性求出最值;(2)设出直线方程,根据|F2C|=|F2D|,可知F2在弦CD的中垂线上,利用中点和斜率关系,写出中垂线方程,代入F2点即可判断.或者根据焦半径公式判断更为简洁.
试题解析:(1)易知a=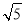 ,b=2,c=1,∴F1(-1,0),F2(1,0)
,b=2,c=1,∴F1(-1,0),F2(1,0)
设P(x,y),则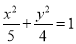
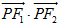 =(-1-x,-y)·(1-x,-y)
=(-1-x,-y)·(1-x,-y)
=x2+y2-1
=x2+4-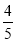 x2-1
x2-1
=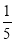 x2+3
x2+3
∵x2∈[0,5],
当x=0,即点P为椭圆短轴端点时,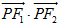 有最小值3;
有最小值3;
当x=±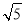 ,即点P为椭圆长轴端点时,
,即点P为椭圆长轴端点时,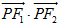 有最大值4.
有最大值4.
(2)法一、假设存在满足条件的直线l,易知点A(5,0)在椭圆外部,当直线斜率不存在时,直线l与椭圆无交点.
所以满足条件的直线斜率存在,设为k
则直线方程为y=k(x-5)
由方程组
得:(5k2+4)x2-50k2x+125k2-20=0
依题意,△=20(16-80k2)>0
得: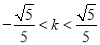
当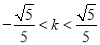 时,设交点为C(x1,y1),D(x2,y2),CD中点为R(x0,y0)
时,设交点为C(x1,y1),D(x2,y2),CD中点为R(x0,y0)
则x1+x2=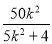 ,x0=
,x0=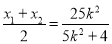
∴y0=k(x0-5)=k(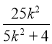 -5)=
-5)=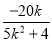
又|F2C|=|F2D|,有F2R⊥l,即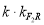 =-1
=-1
即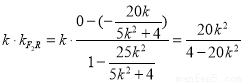 =-1
=-1
即20k2=20k2-4,
该等式不成立,所以满足条件的直线l不存在.
法二、设交点为C(x1,y1),D(x2,y2),
设它们到右准线x=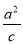 的距离分别为d1、d2,
的距离分别为d1、d2,
根据椭圆第二定义,有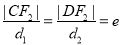
因为|F2C|=|F2D|,故d1=d2,于是x1=x2,
于是CD所在直线l⊥x轴
又直线l经过A(5,0)点,于是l的方程为x=5
但x=5与椭圆无公共点,所以,满足条件的直线不存在.
考点:椭圆的标准方程,直线与椭圆的位置关系,平面向量的数量积,最值,存在性问题


科目:高中数学 来源:2015届四川省高三10月月考理科数学试卷(解析版) 题型:选择题
如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )

A. B.
B.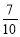 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届四川省高三10月月考文科数学试卷(解析版) 题型:填空题
等比数列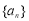 的前
的前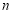 项和为
项和为 ,已知S1,2S2,3S3成等差数列,则数列
,已知S1,2S2,3S3成等差数列,则数列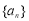 的公比为____________。
的公比为____________。
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:填空题
已知数列{an}(n∈N+)是各项均为正数且公比不等于1的等比数列,对于函数y=f(x),若数列{lnf(an)}为等差数列,则称函数f(x)为“保比差数列函数”.现有定义在(0,+∞)上的四个函数:①f(x)=ex;②f(x)=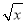 ;③f(x)=kx(k>0);④f(x)=ax2+b(a>0且b>0).则为“保比差数列函数”的是_______________.
;③f(x)=kx(k>0);④f(x)=ax2+b(a>0且b>0).则为“保比差数列函数”的是_______________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:选择题
已知函数f(x)=sin(2x+Φ),其中Φ∈(0,2π),若f(x)≤|f(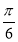 )|对一切x∈R恒成立,且f(
)|对一切x∈R恒成立,且f(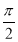 )<f(π),则f(x)的单调递增区间是( )
)<f(π),则f(x)的单调递增区间是( )
A、[kπ+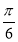 ,kπ+
,kπ+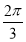 ](k∈Z)
](k∈Z)
B、[kπ-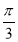 ,kπ+
,kπ+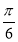 ](k∈Z)
](k∈Z)
C、[kπ,kπ+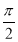 ](k∈Z)
](k∈Z)
D、[kπ-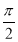 ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:填空题
设f(x)= ,且f(8)=2,则f(f(80))=________________.
,且f(8)=2,则f(f(80))=________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com