已知圆C经过点A(1,0)和B(2,1),且圆心C在直线y=2x-4上.
(1)求圆C的方程;
(2)从点T(3,2)向圆C引切线,求切线长和切线方程;
(3)若点P(a,b)在圆C上,试求a2+(b-2)2的取值范围.
【答案】
分析:(1)由题意可设圆心C(a,2a-4),由AC=BC=r可得(1-a)
2+(2a-4)
2=(2-a)
2+(2a-5)
2,解出a可求圆的方程
(2)设TM,TN分别为圆的切线,在Rt△TCM中,可求TC,r由TM=TN=
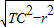
可求
由题意可得直线x=3与该圆相切,设过T的切线的斜率为k,则切线方程为y-2=k(x-3)即kx-y+2-3k=0,由直线与圆相切可得,
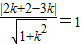
可求k,进而可得过T的切线方程(3)(3)设E(0,2)则PE=
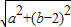
,连接EC与圆交与两点分别记为P
1,P
2,,则可知当P在位置P
1时,PE=EC-r最小,当点P在P
2时,PE=EC+r最大,从而可求a
2+(b-2)
2的取值范围
解答:解:(1)由题意可设圆心C(a,2a-4)
∵AC=BC=r
∴(1-a)
2+(2a-4)
2=(2-a)
2+(2a-5)
2∴a=2,C(2,0),半径r=1
∴圆的方程为(x-2)
2+y
2=1
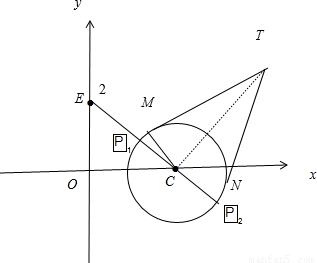
(2)如图所示TM,TN分别为圆的切线
Rt△TCM中,TC=
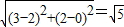
,r=1
∴
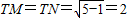
即切线长为2
由题意可得直线x=3与该圆相切
设过T的切线的斜率为k,则切线方程为y-2=k(x-3)即kx-y+2-3k=0
由直线与圆相切可得,
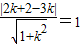
∴
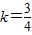
故过T的切线方程分别为x=3或3x-4y-1=0
(3)设E(0,2)则PE=
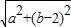
连接EC与圆交与两点分别记为P
1,P
2,如图所示
则可知当P在位置P
1时,PE=EC-1=
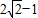
最小,当点P在P
2时,PE=EC+1=
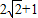
最大
∴a
2+(b-2)
2的取值范围为:[
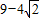
,9+4
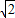
]
 点评:
点评:本题主要考查了利益圆的性质求解圆的方程,考查了圆的切线长的性质及切切方程的求解(注意斜率不存在的情况的考虑)解(3)的关键是结合几何意义转化为求解距离的最大与最小值问题.

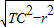 可求
可求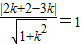 可求k,进而可得过T的切线方程(3)(3)设E(0,2)则PE=
可求k,进而可得过T的切线方程(3)(3)设E(0,2)则PE=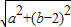 ,连接EC与圆交与两点分别记为P1,P2,,则可知当P在位置P1时,PE=EC-r最小,当点P在P2时,PE=EC+r最大,从而可求a2+(b-2)2的取值范围
,连接EC与圆交与两点分别记为P1,P2,,则可知当P在位置P1时,PE=EC-r最小,当点P在P2时,PE=EC+r最大,从而可求a2+(b-2)2的取值范围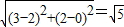 ,r=1
,r=1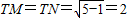 即切线长为2
即切线长为2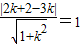 ∴
∴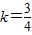
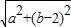
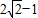 最小,当点P在P2时,PE=EC+1=
最小,当点P在P2时,PE=EC+1=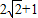 最大
最大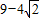 ,9+4
,9+4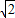 ]
]

