
【题目】已知在四面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,则四面体
,则四面体![]() 外接球的表面积为__________.
外接球的表面积为__________.
【答案】![]()
【解析】由题意可采用割补法,考虑到四面体![]() 的四个面为全等的三角形,所以可在其每个面补上一个以
的四个面为全等的三角形,所以可在其每个面补上一个以![]() ,
,![]() ,
,![]() 为三边的三角形作为底面,分别以x,y,z为侧棱长且两两垂直的三棱锥,从而可得到一个长、宽、高分别为x,y,z的长方体,并且
为三边的三角形作为底面,分别以x,y,z为侧棱长且两两垂直的三棱锥,从而可得到一个长、宽、高分别为x,y,z的长方体,并且![]() 设球半径为
设球半径为![]() ,则有
,则有![]() 所以球的表面积为
所以球的表面积为![]() .
.
点睛: (1)补形法的应用思路:“补形法”是立体几何中一种常见的重要方法,在解题时,把几何体通过“补形”补成一个完整的几何体或置于一个更熟悉的几何体中,巧妙地破解空间几何体的体积等问题,常见的补形法有对称补形、联系补形与还原补形,对于还原补形,主要涉及台体中“还台为锥”.
(2)补形法的应用条件:当某些空间几何体是某一个几何体的一部分,且求解的问题直接求解较难入手时,常用该法.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线y=x2﹣6x+5与坐标轴的交点都在圆C上.
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C与直线x﹣y+a=0交于A,B两点,且CA⊥CB求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
(Ⅰ)证明:A1C1=AB1;
(Ⅱ)若AC⊥AB1 , ∠BCC1=120°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.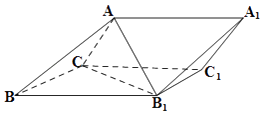
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取![]() 件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表
内,则为合格品,否则为不合格品.表![]() 是甲流水线样本的频数分布表,图
是甲流水线样本的频数分布表,图![]() 是乙流水线样本的频率分布直方图.
是乙流水线样本的频率分布直方图.
表 | ||||||||||||
|
图 |
|
(Ⅰ)根据图![]() ,估计乙流水线生产产品该质量指标值的中位数.
,估计乙流水线生产产品该质量指标值的中位数.
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了![]() 件产品,则甲,乙两条流水线分别生产出不合格品约多少件.
件产品,则甲,乙两条流水线分别生产出不合格品约多少件.
(Ⅲ)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:  (其中
(其中![]() 样本容量)
样本容量)
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示.
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少? 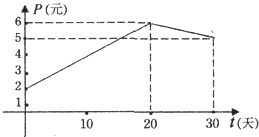
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com