
如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=600,E为PA的中点,F为PC上不同于P、C的任意一点.
(1)求证:PC∥面EBD
(2)求异面直线AC与PB间的距离
(3)求三棱锥E-BDF的体积.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
(12分)(2011•陕西)如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把是BC上的△ABD折起,使∠BDC=90°.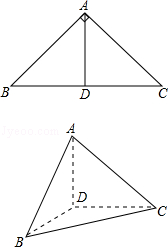
(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设BD=1,求三棱锥D﹣ABC的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·贵阳模拟)一个几何体是由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在圆O的圆周上,其正(主)视图,侧(左)视图的面积分别为10和12,如图所示,其中EA⊥平面ABC,AB⊥AC,AB=AC.AE=2.
(1)求证:AC⊥BD.
(2)求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图甲,在平面四边形ABCD中,已知
 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
(1)求证:DC 平面ABC;
平面ABC;
(2)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,直三棱柱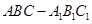 中,
中,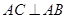 ,
, 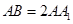 ,
,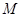 是
是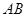 的中点,△
的中点,△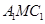 是等腰三角形,
是等腰三角形,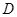 为
为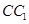 的中点,
的中点,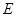 为
为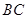 上一点.
上一点.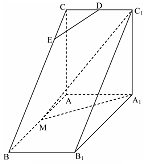
(1)若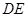 ∥平面
∥平面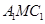 ,求
,求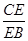 ;
;
(2)平面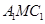 将三棱柱
将三棱柱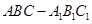 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图甲,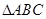 是边长为6的等边三角形,
是边长为6的等边三角形,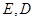 分别为
分别为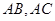 靠近
靠近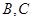 的三等分点,点
的三等分点,点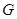 为边
为边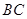 边的中点,线段
边的中点,线段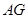 交线段
交线段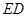 于点
于点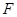 .将
.将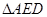 沿
沿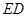 翻折,使平面
翻折,使平面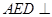 平面
平面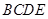 ,连接
,连接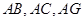 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.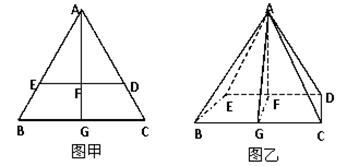
(1)求证: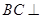 平面
平面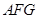
(2)求四棱锥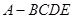 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com