若函数h(x)＝2x－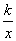
＋
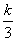在(1，＋∞)上是增函数，则实数k的取值范围是( )
A．[－2，＋∞) B．[2，＋∞)
C．(－∞，－2] D．(－∞，2]
科目：高中数学 来源： 题型：
函数f(x)的定义域为A，若x1，x2∈A，且f(x1)＝f(x2)时总有x1＝x2，则称f(x)为单函数．例如，函数f(x)＝2x＋1(x∈R)是单函数，下列命题：
①函数f(x)＝x2(x∈R)是单函数；
②若f(x)为单函数，x1，x2∈A且x1≠x2，则f(x1)≠f(x2)；
③若f：A→B为单函数，则对于任意b∈B，它至多有一个原像；
④函数f(x)在某区间上具有单调性，则f(x)一定是单函数．
其中的真命题是________．(写出所有真命题的编号)
查看答案和解析>>
科目：高中数学 来源： 题型：
某化工厂生产某种产品，每件产品的生产成本是3元，根据市场调查，预计每件产品的出厂价为x元(7≤x≤10)时，一年的产量为(11－x)2万件，若该企业所生产的产品全部售出，则称该企业正常生产，但为了保护环境，用于治理污染的费用与产量成正比，比例系数为常数a(1≤a≤3)．
(1)求该企业正常生产一年的利润L(x)与出厂价x的函数关系式；
(2)当每件产品的出厂价定为多少元时，企业一年的利润最大，并求最大利润．
查看答案和解析>>
科目：高中数学 来源： 题型：
“a≤0”是“函数f(x)＝|(ax－1)x|在区间(0，＋∞)内单调递增”的 ( )
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源： 题型：
已知定义在区间(0，＋∞)上的函数f(x)满足f(
)＝f(x1)－f(x2)，且当x>1时，f(x)>0.
(1)求f(1)的值，并判断f(x)的单调性；
(2)若f(4)＝2，求f(x)在[5,16]上的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知y＝f(x)是定义在R上的偶函数，且f(x)在(0，＋∞)上是增函数，如果x1<0，x2>0，且|x1|<|x2|，则有( )
A．f(－x1)＋f(－x2)>0 B．f(x1)＋f(x2)<0
C．f(－x1)－f(－x2)>0 D．f(x1)－f(x2)<0
查看答案和解析>>
科目：高中数学 来源： 题型：
设偶函数f(x)对任意x∈R，都有f(x＋3)＝－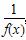
，且当x∈[－3，－2]时，f(x)＝4x，则f(107.5)＝( )
A．10 B.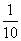
C．－10 D．－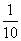
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
)＝0，则满足f(log
x)>0的x的集合为________．
的图象大致是( )