Question

【题目】已知函数，其中.

（1）求函数的单调递增区间；

（2）若函数在上有且只有一个零点，求实数的取值范围.

Answer 1

【答案】（1）详见解析；（2）.

【解析】

试题（1）先求函数的定义域与导数，对是否在定义域内以及在定义域内与进行大小比较，从而确定函数的单调区间；（2）在（1）的条件下结合函数的单调性与零点存在定理对端点值或极值的正负进行限制，从而求出参数的取值范围.

试题解析：（1）函数定义域为，

，

①当，即时，

令，得，函数的单调递减区间为，

令，得，函数的单调递增区间为；

②当，即时，

令，得或，函数的单调递增区间为，，

令，得，函数的单调递减区间为；

③当，即时，恒成立，函数的单调递增区间为；

（2）①当时，由（1）可知，函数的单调递减区间为，在单调递增，

所以在上的最小值为，

由于，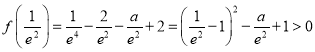

要使在上有且只有一个零点，

需满足或，解得或，

所以当或时，在上有且只有一个零点；

②当时，由（1）可知，函数在上单调递增，

且，，

所以当时，在上有且只有一个零点；

③当时，由（1）可知，函数在内单调递增，在上单调递减，在上单调递增，

又因为，所以当时，总有，

因为，

所以，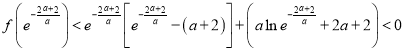

所以在区间内必有零点，

又因为在内单调递增，

从而当时，在上有且只有一个零点，

综上所述，当或或时，在上有且只有一个零点.