
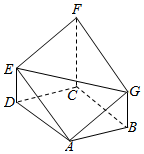
 在如图所示的多面体ABCDEFG中,面ABCD是边长为2的菱形,∠BAD=120°,DE∥CF∥BG,CF⊥面ABCD,AG∥EF,且CF=2 BG=4.
在如图所示的多面体ABCDEFG中,面ABCD是边长为2的菱形,∠BAD=120°,DE∥CF∥BG,CF⊥面ABCD,AG∥EF,且CF=2 BG=4.分析 (Ⅰ)证明四边形AEFG为平行四边形.连接AF交EG于M,连接AC,BD交于O,连接MO,证明MG∥BO.即可证明EG∥平面ABCD.
(Ⅱ)解法一、证明FC与平面AEFG所成的角就是∠AFC.在Rt△AFC中,求解FC与平面AEG所成角的正弦即可.
解法二、以O为坐标原点,分别以直线AC、BD为x、y轴,建立空间直角坐标系O-xyz,求出平面AEG的法向量,然后利用向量的数量积求解直线CF与平面AEG所成角的正弦值即可.
解答 解:(Ⅰ)证明:AG∥EF⇒AG与EF共面.
由平面ADE∥平面BCFG⇒AE∥FG⇒
四边形AEFG为平行四边形.
连接AF交EG于M,连接AC,BD交于O,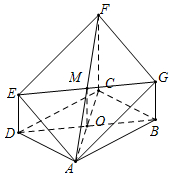
连接MO,如图1所示.
则MO∥CF,且$MO=\frac{1}{2}CF=BG$,
故BOMG为平行四边形,所以MG∥BO.
又BO?平面ABCD,MG?平面ABCD,
所以MG∥平面ABCD,即EG∥平面ABCD.…(6分)
(Ⅱ)解法一、DE∥CF∥BG,CF⊥面ABCD,AG∥EF,
$\left.{\begin{array}{l}{CF⊥平面ABCD⇒CF⊥DB}\\{四边形ABCD是菱形⇒BD⊥AC}\\{CF、AC?面ABCD且CF∩AC=O}\end{array}}\right\}$⇒BD⊥平面ACF.
由(Ⅰ)知EG∥BD,所以EG⊥平面ACF⇒平面AEFG⊥平面ACF.
因为平面AEFG∩平面ACF=AF,C∈平面ACF,所以点C在平面AEFG
内的射影落在AF上,故FC与平面AEFG所成的角就是∠AFC.
在Rt△AFC中,$sin∠AFC=\frac{AC}{AF}=\frac{2}{{\sqrt{{2^2}+{4^2}}}}=\frac{{\sqrt{5}}}{5}$,
所以FC与平面AEG所成角的正弦为$\frac{{\sqrt{5}}}{5}$.…(12分)
解法二、
由(Ⅰ)易知,DE=BG=2.以O为坐
标原点,分别以直线AC、BD为x、y
轴,建立空间直角坐标系O-xyz,
如图2所示.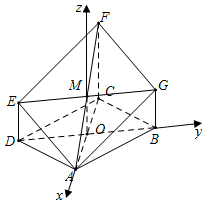
则有A(1,0,0)、$E(0\;,\;-\sqrt{3}\;,\;\;2)$,$G(0\;,\;\sqrt{3}\;,\;2)$,C(-1,0,0),F(-1,0,4),
所以 $\overrightarrow{AE}=(-1\;,\;\;-\sqrt{3}\;,\;\;2)$,$\overrightarrow{EG}=(0\;,\;\;2\sqrt{3}\;,\;\;0)$,$\overrightarrow{CF}=(0\;,\;0\;,\;4)$.
设面AEG的法向量为$\overrightarrow n=(x\;,\;y\;,\;z)$,
由$\overrightarrow n⊥\overrightarrow{AE}$,$\overrightarrow n⊥\overrightarrow{EG}$,得$\left\{\begin{array}{l}-x-\sqrt{3}y+2z=0\;\\ 2\sqrt{3}y=0.\end{array}\right.$令z=1,则x=2
所以$\overrightarrow n=(2\;,\;0\;,\;1)$,于是$cos<\overrightarrow n\;,\;\overrightarrow{CF}>=\frac{4}{{4\sqrt{5}}}=\frac{{\sqrt{5}}}{5}$.…(10分)
故直线CF与平面AEG所成角的正弦值为$\frac{{\sqrt{5}}}{5}$.…(12分)
点评 本题考查直线与平面平行于垂直的判定定理的应用,直线与平面所成角的求法,考查空间想象能力以及计算能力.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=2是x2-4x+4=0的必要不充分条件 | |
| B. | 在△ABC中,三边a,b,c所对的角分别为A,B,C,若acosA=bcosB,则该三角形△ABC为等腰三角形 | |
| C. | 命题“若x2<4,则-2<x<2”的逆否命题为“若x2≥4,则x≥2或x≤-2” | |
| D. | 若p∧(¬q)为假,p∨(¬q)为真,则p,q同真或同假 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\frac{2\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{7}$ | B. | $\frac{6}{5}$ | C. | $\frac{7}{8}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com