
分析 所求的式子cosC利用二倍角的余弦函数公式化简后,将已知的cos$\frac{C}{2}$的值代入即可求出cosC值,利用余弦定理分别表示出cosB和cosA,代入到已知的等式中,化简后即可求出c的值,然后利用余弦定理表示出c2=a2+b2-2abcosC,把c及cosC的值代入后,利用基本不等式即可求出ab的最大值,然后由cosC的值,及C的范围,利用同角三角函数间的基本关系求出sinC的值,利用三角形的面积公式表示出三角形ABC的面积,把ab的最大值及sinC的值代入即可求出面积的最大值.
解答 (本题满分为14分)
解:∵cos$\frac{C}{2}$=$\frac{\sqrt{5}}{3}$,
∴cosC=2cos2$\frac{C}{2}$-1=2($\frac{\sqrt{5}}{3}$)2-1=$\frac{1}{9}$;…(7分)
∵acosB+bcosA=2,
∴a×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$+b×$\frac{{c}^{2}+{b}^{2}-{a}^{2}}{2bc}$=2,
∴c=2,…(9分)
∴4=a2+b2-2ab×$\frac{1}{9}$≥2ab-2ab×$\frac{1}{9}$=$\frac{16}{9}$ab,
∴ab≤$\frac{9}{4}$(当且仅当a=b=$\frac{3}{2}$时等号成立)…(12分)
由cosC=$\frac{1}{9}$,得sinC=$\frac{4\sqrt{5}}{9}$…(13分)
∴S△ABC=$\frac{1}{2}$absinC≤$\frac{1}{2}$×$\frac{9}{4}$×$\frac{4\sqrt{5}}{9}$=$\frac{\sqrt{5}}{2}$,
故△ABC的面积最大值为$\frac{\sqrt{5}}{2}$…(14分)
点评 此题考查了二倍角的余弦函数公式,基本不等式,余弦定理及三角形的面积公式.熟练掌握公式及定理是解本题的关键.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
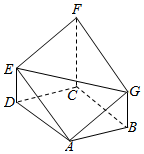 在如图所示的多面体ABCDEFG中,面ABCD是边长为2的菱形,∠BAD=120°,DE∥CF∥BG,CF⊥面ABCD,AG∥EF,且CF=2 BG=4.
在如图所示的多面体ABCDEFG中,面ABCD是边长为2的菱形,∠BAD=120°,DE∥CF∥BG,CF⊥面ABCD,AG∥EF,且CF=2 BG=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | (1,0) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某单位在对一个长800m、宽600m的草坪进行绿化时,是这样想的:中间为矩形绿草坪,四周是等宽的花坛,如图所示,若要保证绿草坪的面积不小于总面积的二分之一.试确定花坛宽度的取值范围.
某单位在对一个长800m、宽600m的草坪进行绿化时,是这样想的:中间为矩形绿草坪,四周是等宽的花坛,如图所示,若要保证绿草坪的面积不小于总面积的二分之一.试确定花坛宽度的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com