
| A. | x=2是x2-4x+4=0的必要不充分条件 | |
| B. | 在△ABC中,三边a,b,c所对的角分别为A,B,C,若acosA=bcosB,则该三角形△ABC为等腰三角形 | |
| C. | 命题“若x2<4,则-2<x<2”的逆否命题为“若x2≥4,则x≥2或x≤-2” | |
| D. | 若p∧(¬q)为假,p∨(¬q)为真,则p,q同真或同假 |
分析 A根据定义判断即可;
B利用正弦定理和诱导公式判断;
C根据逆否命题的定义判断;
D根据或命题和且命题以及非命题的等价关系可判断.
解答 解:A中x=2能推出x2-4x+4=0,但反之不一定,故应是充分不必要条件,故错误;
B中在△ABC中,三边a,b,c所对的角分别为A,B,C,若acosA=bcosB,由正弦定理可得sinAcosA=sinBcosB,
∴sin2A=sin2B,故A=B或A+B=$\frac{π}{2}$,则该三角形△ABC为等腰三角形或直角三角形,故错误;
C中命题“若x2<4,则-2<x<2”的逆否命题为“若x≥2或x≤-2,则x2≥4,”故错误;
D根据或命题和且命题以及非命题的等价关系可判断是正确的.
点评 考查了四中命题的逻辑关系和三角函数中正弦定理和诱导公式的应用.属于基础题型,应熟练掌握.


科目:高中数学 来源: 题型:选择题
| A. | 4a-2m | B. | 4a | C. | 4a+m | D. | 4a+2m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | $\frac{{8\sqrt{2}}}{3}π$ | C. | $\frac{{8\sqrt{3}}}{3}π$ | D. | $\frac{16}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
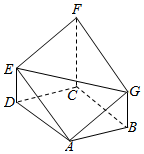 在如图所示的多面体ABCDEFG中,面ABCD是边长为2的菱形,∠BAD=120°,DE∥CF∥BG,CF⊥面ABCD,AG∥EF,且CF=2 BG=4.
在如图所示的多面体ABCDEFG中,面ABCD是边长为2的菱形,∠BAD=120°,DE∥CF∥BG,CF⊥面ABCD,AG∥EF,且CF=2 BG=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | (1,0) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com