Question

1．四面体ABCD的四个顶点都在球O的球面上，AB=2，BC=CD=1，∠BCD=60°，AB⊥平面BCD，则球O的表面积为（　　）

• A． 8π
• B． $\frac{{8\sqrt{2}}}{3}π$
• C． $\frac{{8\sqrt{3}}}{3}π$
• D． $\frac{16}{3}π$

Answer 1

分析 由题意画出图形，设出底面三角形的外心G，找出四面体ABCD的外接球的球心O，通过求解直角三角形得到三棱锥的高，则答案可求．

解答 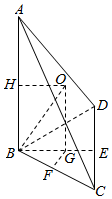解：如图，∵BC=CD=1，∠BCD=60°
∴底面△BCD为等边三角形
取CD中点为E，连接BE，
∴△BCD的外心G在BE上，设为G，取BC中点F，连接GF，
在Rt△BCE中，由CE=$\frac{1}{2}$，∠CBE=30°，得BF=$\frac{1}{2}BC$=$\frac{1}{2}$，
又在Rt△BFG中，得BG=$\frac{\frac{1}{2}}{cos30°}=\frac{\sqrt{3}}{3}$，
过G作AB的平行线与AB的中垂线HO交于O，
则O为四面体ABCD的外接球的球心，即R=OB，
∵AB⊥平面BCD，∴OG⊥BG，
在Rt△BGO中，求得OB=$\sqrt{O{G}^{2}+B{G}^{2}}=\sqrt{{1}^{2}+（\frac{\sqrt{3}}{3}）^{2}}=\frac{2\sqrt{3}}{3}$，
∴球O的表面积为$4π•（\frac{2\sqrt{3}}{3}）^{2}=\frac{16π}{3}$．
故选：D．

点评 本题考查球的表面积的求法，是中档题，解题时要认真审题，注意构造法的合理运用．