
【题目】甲乙两人参加某种选拔测试,在备选的10道题中,甲答对其中每道题的概率都是![]() ,乙能答对其中的8道题.规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选;
,乙能答对其中的8道题.规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选;
(Ⅰ)求甲恰有2个题目答对的概率及甲答对题目数![]() 的数学期望与方差。
的数学期望与方差。
(Ⅱ)求乙答对的题目数X的分布列。
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为:
的参数方程为: 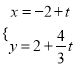 (t为参数),它与曲线C:
(t为参数),它与曲线C: ![]() 相交于A,B两点.
相交于A,B两点.
(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,且x<0时,f(x)=1+2x.
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图像;
(3)写出函数f(x)的单调区间及值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 恒过的定点
恒过的定点![]() 的坐标;
的坐标;
(Ⅱ)在(Ⅰ)的条件下,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线y=Asin(ωx+φ)(A>0,ω>0)上的一个最高点的坐标为(![]() ,
,![]() ),由此点到相邻最低点间的曲线与x轴交于点(
),由此点到相邻最低点间的曲线与x轴交于点(![]() π,0),φ∈(﹣
π,0),φ∈(﹣![]() ,
,![]() ).
).
(1)求这条曲线的函数解析式;
(2)写出函数的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量m=(cosx,-1),n=![]() ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m.
(1)求函数f(x)的最小正周期;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=1,c=![]() ,且f(A)恰是函数f(x)在
,且f(A)恰是函数f(x)在![]() 上的最大值,求A,b和△ABC的面积.
上的最大值,求A,b和△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由9名高二级学生和6名高一级学生组成,现采用分层抽样的方法抽取5人,组成一个体验小组去市场体验“共享单车”的使用.问:
(Ⅰ)应从该兴趣小组中抽取高一级和高二级的学生各多少人;
(Ⅱ)已知该地区有![]() ,
, ![]() 两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租
两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租![]() 型车,高一级学生都租
型车,高一级学生都租![]() 型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租
型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租![]() 型车的概率.
型车的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com