
【题目】已知曲线y=Asin(ωx+φ)(A>0,ω>0)上的一个最高点的坐标为(![]() ,
,![]() ),由此点到相邻最低点间的曲线与x轴交于点(
),由此点到相邻最低点间的曲线与x轴交于点(![]() π,0),φ∈(﹣
π,0),φ∈(﹣![]() ,
,![]() ).
).
(1)求这条曲线的函数解析式;
(2)写出函数的单调区间.
【答案】(1)y=![]() sin(
sin(![]() x+
x+![]() );(2)[4kπ+
);(2)[4kπ+![]() ,4kπ+
,4kπ+![]() ],k∈Z.
],k∈Z.
【解析】解:(1)由题意可得A=![]() ,
,![]()
![]() =
=![]() ﹣
﹣![]() ,求得ω=
,求得ω=![]() .
.
再根据最高点的坐标为(![]() ,
,![]() ),可得
),可得![]() sin(
sin(![]() ×
×![]() +φ)=
+φ)=![]() ,即sin(
,即sin(![]() ×
×![]() +φ)=1 ①.
+φ)=1 ①.
再根据由此最高点到相邻最低点间的曲线与x轴交于点(![]() π,0),可得得
π,0),可得得![]() sin(
sin(![]() ×
×![]() +φ)=0,即sin(
+φ)=0,即sin(![]() +φ)=0 ②,
+φ)=0 ②,
由①②求得φ=![]() ,故曲线的解析式为y=
,故曲线的解析式为y=![]() sin(
sin(![]() x+
x+![]() ).
).
(2)对于函数y=![]() sin(
sin(![]() x+
x+![]() ),令2kπ﹣
),令2kπ﹣![]() ≤
≤![]() +
+![]() ≤2kπ+
≤2kπ+![]() ,求得4kπ﹣
,求得4kπ﹣![]() ≤x≤4kπ+
≤x≤4kπ+![]() ,
,
可得函数的增区间为[4kπ﹣![]() ,4kπ+
,4kπ+![]() ],k∈Z.
],k∈Z.
令2kπ+![]() ≤
≤![]() +
+![]() ≤2kπ+
≤2kπ+![]() ,求得4kπ+
,求得4kπ+![]() ≤x≤4kπ+
≤x≤4kπ+![]() ,
,
可得函数的减区间为[4kπ+![]() ,4kπ+
,4kπ+![]() ],k∈Z.
],k∈Z.


科目:高中数学 来源: 题型:
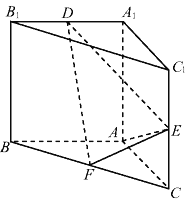
【题目】直三棱柱![]() 中,
中, ![]()
![]() 分别是
分别是![]() 的中点, 且
的中点, 且![]() ,
,
(1)证明: ![]() .
.
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() 若存在,说明点
若存在,说明点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 的图象与x轴无交点,求a的取值范围;
的图象与x轴无交点,求a的取值范围;
(2) 若函数![]() 在[-1,1]上存在零点,求a的取值范围;
在[-1,1]上存在零点,求a的取值范围;
(3)设函数![]() ,当
,当![]() 时,若对任意的
时,若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求b的取值范围.
,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人参加某种选拔测试,在备选的10道题中,甲答对其中每道题的概率都是![]() ,乙能答对其中的8道题.规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选;
,乙能答对其中的8道题.规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选;
(Ⅰ)求甲恰有2个题目答对的概率及甲答对题目数![]() 的数学期望与方差。
的数学期望与方差。
(Ⅱ)求乙答对的题目数X的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
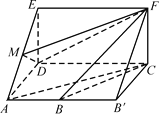
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,![]() ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面MDF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 过椭圆
过椭圆![]() :
: ![]() (
(![]() )的短轴端点,
)的短轴端点, ![]() ,
, ![]() 分别是圆
分别是圆![]() 与椭圆
与椭圆![]() 上任意两点,且线段
上任意两点,且线段![]() 长度的最大值为3.
长度的最大值为3.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作圆
作圆![]() 的一条切线交椭圆
的一条切线交椭圆![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com