【题目】直三棱柱中, 分别是的中点, 且,

(1)证明: .

(2)棱上是否存在一点,使得平面与平面所成锐二面角的余弦值为若存在,说明点的位置,若不存在,说明理由.

参考答案：

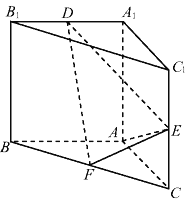
【答案】（1）见解析（2）点D为A1B1中点

【解析】试题分析：（1）由直三棱柱性质可得AB⊥AA1,根据条件可得AB⊥AE.最后根据线面垂直判定定理证明结论（2）研究二面角大小一般利用空间向量数量积，即先建立空间直角坐标系，设立各点坐标，利用方程组解各面法向量，再根据向量数量积求法向量夹角，根据法向量夹角与二面角关系建立方程，解出点的坐标，确定其位置

试题解析：(1)∵AE⊥A1B1,A1B1∥AB,

∴AB⊥AE.

又∵AB⊥AA1,AE∩AA1=A,

∴AB⊥平面A1ACC1.

(2) ∵ AB⊥平面A1ACC1.

又∵AC平面A1ACC1,

∴AB⊥AC.

以A为原点建立如图所示的空间直角坐标系Axyz.

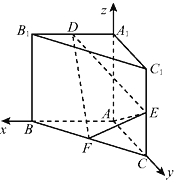
则A(0,0,0),E,F,0,A1(0,0,1),B1(1,0,1).

假设存在, =λ,且λ∈[0,1],

∴D(λ,0,1).

设平面DEF的法向量为n=(x,y,z),

则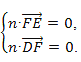

∵,

∴

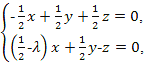
即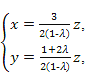

令z=2(1-λ),

∴n=(3,1+2λ,2(1-λ)).

由题可知平面ABC的一个法向量m=(0,0,1).

∵平面DEF与平面ABC所成锐二面角的余弦值为,

∴|cos(m,n)|=,

即.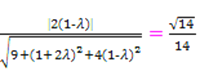

∴λ=或λ= (舍),

∴当点D为A1B1中点时,满足要求.

关闭