
【题目】设![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求![]() 的值;
的值;
(2)若对于任意的![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)求证: ![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)详见解析
(Ⅲ)详见解析
【解析】试题分析:(Ⅰ)先求导数,再根据导数几何意义列方程,解方程可得![]() 的值;(Ⅱ)不等式恒成立问题,一般转化为对应函数最值问题,本题去分母转化为差函数:
的值;(Ⅱ)不等式恒成立问题,一般转化为对应函数最值问题,本题去分母转化为差函数: ![]() ,因为
,因为![]() ,所以
,所以![]() 最大值不小于
最大值不小于![]() ,根据
,根据![]() 导函数符号可得
导函数符号可得![]() 才满足条件.(Ⅲ)不等式证明中涉及求和问题,一般方法为适当放缩,再利用裂项相消法给予证明.本题由(Ⅱ)知,当
才满足条件.(Ⅲ)不等式证明中涉及求和问题,一般方法为适当放缩,再利用裂项相消法给予证明.本题由(Ⅱ)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立,所以放缩这一难点已暗示,下面只需令
成立,所以放缩这一难点已暗示,下面只需令![]() 得
得![]() ,即
,即![]() ,最后叠加可得证.
,最后叠加可得证.
试题解析:(Ⅰ) 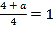
由题设![]() ,∴
,∴![]()
![]() .
.
(Ⅱ)![]() ,
,![]() ,
, ![]() ,即
,即![]()
设![]() ,即
,即![]() .
.
![]()
![]()
①若![]() ,
, ![]() ,这与题设
,这与题设![]() 矛盾
矛盾
②若![]() 当
当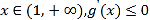 ,
, ![]() 单调递增,
单调递增, ![]() ,与题设矛盾.
,与题设矛盾.
③若![]() 当
当![]() ,
, ![]() 单调递减,
单调递减, ![]() ,即不等式成立
,即不等式成立
综上所述, ![]() .
.
(Ⅲ)由(Ⅱ)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立.
成立.
不妨令![]() 所以
所以![]() ,
,
![]()
![]()
![]()
…………
![]()
累加可得
∴![]()


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知6只小白鼠有1只被病毒感染,需要通过对其化验病毒![]() 来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒
来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒![]() ,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒
,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒![]() ,则在另外一组中逐个进行化验.
,则在另外一组中逐个进行化验.
(1)求依据方案乙所需化验恰好为2次的概率.
(2)首次化验化验费为10元,第二次化验化验费为8元,第三次及其以后每次化验费都是6元,列出方案甲所需化验费用的分布列,并估计用方案甲平均需要体验费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列对应是否为集合A到集合B的函数.
(1)A=R,B={x|x>0},f:x→y=|x|;
(2)A=Z,B=Z,f:x→y=x2;
(3)A=Z,B=Z,f:x→y=![]() ;
;
(4)A={x|-1≤x≤1},B={0},f:x→y=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
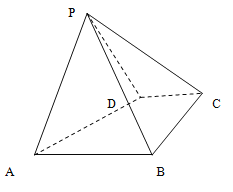
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(Ⅰ)证明:![]()
(Ⅱ)若四棱锥![]() 的体积等于
的体积等于![]() .问:是否存在过点
.问:是否存在过点![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.

(1)求证:GH∥平面CDE;
(2)求证:面ADEF⊥面ABCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家刘徽是公元三世纪世界上最杰出的数学家,他在《九章算术圆田术》注中,用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法.所谓“割圆术”,即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率(圆周率指圆周长与该圆直径的比率).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径![]()
,此时圆内接正六边形的周长为![]()
,此时若将圆内接正六边形的周长等同于圆的周长,可得圆周率为3,当用正二十四边形内接于圆时,按照上述算法,可得圆周率为__________.(参考数据: ![]()
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的![]() 倍和
倍和![]() 倍后,得到曲线
倍后,得到曲线![]()
(1)试写出曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求点
上求点![]() ,使得点
,使得点![]() 到直线
到直线![]() 的距离最大,并求距离最大值.
的距离最大,并求距离最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com