
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
分析 先利用三角恒等变换化简函数f(x)的解析式,从而求得f($\frac{π}{24}$)的值.
解答 解:∵函数f(x)=sinxcosx-$\frac{\sqrt{3}}{2}$cos2x=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x=sin(2x-$\frac{π}{3}$),
则f($\frac{π}{24}$)=sin($\frac{π}{12}$-$\frac{π}{3}$)=sin(-$\frac{π}{4}$)=-sin$\frac{π}{4}$=-$\frac{\sqrt{2}}{2}$,
故选:A.
点评 本题主要考查三角恒等变换,求函数的值,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
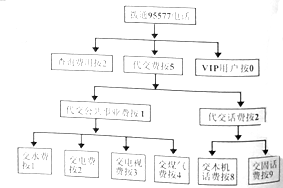 某银行推出95577服务电话,部分业务流程如图,如果我要利用这个服务交纳电视费,请问按照这个流程图,我拨通95577电话后如何操作( )
某银行推出95577服务电话,部分业务流程如图,如果我要利用这个服务交纳电视费,请问按照这个流程图,我拨通95577电话后如何操作( )| A. | 按2,按1,按3 | B. | 按5,按1,按3 | C. | 按0,按2,按1,按3 | D. | 按5,按1,按2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,四边形ABCD是等腰梯形,其中AB∥CD,AB=$\frac{1}{2}$CD=3,且∠BCD=60°;E为CD中点,PA=PB=PC=PD=4.
如图,四棱锥P-ABCD中,四边形ABCD是等腰梯形,其中AB∥CD,AB=$\frac{1}{2}$CD=3,且∠BCD=60°;E为CD中点,PA=PB=PC=PD=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com