
分析 (Ⅰ)设S(x,y),利用定点A(-m,0),B(m,0),S为一动点,点S与A,B两点连线的斜率之积为-$\frac{1}{m^2}$,建立方程,化简求动点S的轨迹C的方程,结合实数m>1,可得曲线类型;
(Ⅱ)当m=$\sqrt{2}$时,求出椭圆C的方程.由直线l:2x-y+t=0(t>0)与曲线C联立得9x2+8tx+2t2-2=0,当△=64t2-36×2(t2-1)=0时,得t=3.此时直线l与曲线C有且只有一个交点;当△=64t2-36×2(t2-1)>0,且直线2x-y+t=0恰好过点(-$\sqrt{2}$,0)时,t=2$\sqrt{2}$,此时直线l与曲线C有且只有一个交点.
(Ⅲ)直线l方程为2x-y+3=0.设点P(a,2a+3),a<2,d1表示P到点(1,0)的距离,d2表示P到直线x=2的距离,则$\frac{{d}_{1}}{{d}_{2}}$=$\sqrt{5•\frac{{a}^{2}+10a+10}{(a-2)^{2}}}$,由此能证明$\frac{{d}_{1}}{{d}_{2}}$的最小值等于椭圆的离心率.
解答 (Ⅰ)解:设S(x,y),则
∵定点A(-m,0),B(m,0),S为一动点,点S与A,B两点连线的斜率之积为-$\frac{1}{m^2}$,
∴$\frac{y}{x+m}•\frac{y}{x-m}$=-$\frac{1}{m^2}$,
∴$\frac{{x}^{2}}{{m}^{2}}$+y2=1,
∵m>1,
∴动点S的轨迹C表示椭圆;
(Ⅱ)解当m=$\sqrt{2}$时,椭圆方程为$\frac{{x}^{2}}{2}$+y2=1.
由直线l:2x-y+t=0(t>0)与曲线C联立得9x2+8tx+2t2-2=0,
当△=64t2-36×2(t2-1)=0时,t=±3,
∵t>0,∴t=3.此时直线l与曲线C有且只有一个交点;
当△=64t2-36×2(t2-1)>0,且直线2x-y+t=0恰好过点(-$\sqrt{2}$,0)时,
t=2$\sqrt{2}$,此时直线l与曲线C有且只有一个交点.
综上,当t=3或t=2$\sqrt{2}$时,直线l与曲线C有且只有一个交点.
(Ⅲ)证明:直线l方程为2x-y+3=0.
设点P(a,2a+3),a<2,d1表示P到点(1,0)的距离,d2表示P到直线x=2的距离,
则d1=$\sqrt{(a-1)^{2}+(2a+3)^{2}}$=$\sqrt{5{a}^{2}+10a+10}$,d2=2-a,
∴$\frac{{d}_{1}}{{d}_{2}}$=$\sqrt{5•\frac{{a}^{2}+10a+10}{(a-2)^{2}}}$,
令f(a)=$\frac{{a}^{2}+2a+2}{(a-2)^{2}}$,则f′(a)=-$\frac{6a+8}{(a-2)^{3}}$,
令f′(a)=0,得a=-$\frac{4}{3}$,
∵当a<-$\frac{4}{3}$时,f′(a)<0;
当-$\frac{4}{3}$<a<2时,f′(a)>0,
∴f(a)在a=-$\frac{4}{3}$时,取得最小值,即$\frac{{d}_{1}}{{d}_{2}}$取得最小值$\sqrt{5f(-\frac{4}{3})}$=$\frac{\sqrt{2}}{2}$,
又椭圆C有离心率为$\frac{\sqrt{2}}{2}$,
∴$\frac{{d}_{1}}{{d}_{2}}$的最小值等于椭圆的离心率.
点评 本题考查椭圆方程的求法,考查直线与椭圆C有且只有一个交点时实数值的求法,考查直线上横坐标小于2的点P到点(1,0)的距离与到直线x=2的距离之比的最小值等于椭圆的离心率的证明,解题时要注意函数与方程思想的合理运用.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
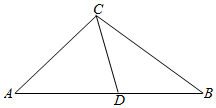 如图:在△ABC中,D为AB边上一点,DA=DC,已知∠B=$\frac{π}{4}$,BC=3
如图:在△ABC中,D为AB边上一点,DA=DC,已知∠B=$\frac{π}{4}$,BC=3查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com