
分析 (1)任取1≤x1<x2,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易得出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案.
(2)利用函数的单调性,即可求f(x)在[1,4]上的最大值及最小值.
解答 解:(1)设1≤x1<x2,f(x2)-f(x1)=${x}_{2}+\frac{1}{{x}_{2}}$-x1-$\frac{1}{{x}_{1}}$=$\frac{({x}_{2}-{x}_{1})({x}_{2}{x}_{1}-1)}{{x}_{2}{x}_{1}}$,
因为1≤x1<x2,所以x2-x1>0,x2x1-1>0,x2x1>0,
所以f(x2)-f(x1)>0,即f(x2)>f(x1)
故函数f(x)在区间[1,+∞)上是增函数;
(2)由(1),可得f(x)在[1,4]上的最大值是f(4)=$\frac{17}{4}$,最小值f(1)=2.
点评 本题考查的知识点是函数单调性的判断与证明,其中作差法(定义法)证明函数的单调性是我们中学阶段证明函数单调性最重要的方法,一定要掌握其解的格式和步骤.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-2,+∞) | C. | (-∞,-$\frac{3}{2}$)∪(-1,+∞) | D. | (-2,-$\frac{3}{2}$)∪(-$\frac{3}{2}$,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{2}$,$\frac{23}{6}$] | B. | ($\frac{5}{2}$,$\frac{23}{6}$) | C. | ($\frac{3}{2}$,$\frac{19}{6}$) | D. | ($\frac{3}{2}$,$\frac{19}{6}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
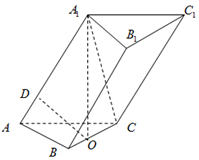 三棱柱ABC-A1B1C1的底面ABC是等边三角形,BC的中点为O,A1O⊥底面ABC,AA1与底面ABC所成的角为$\frac{π}{3}$,点D在棱AA1上,且AD=$\sqrt{3}$,AB=4.
三棱柱ABC-A1B1C1的底面ABC是等边三角形,BC的中点为O,A1O⊥底面ABC,AA1与底面ABC所成的角为$\frac{π}{3}$,点D在棱AA1上,且AD=$\sqrt{3}$,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{8\sqrt{3}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{16\sqrt{3}}}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com