
【题目】如图所示的几何体中,![]() 为直三棱柱,四边形
为直三棱柱,四边形![]() 为平行四边形,
为平行四边形,![]() ,
, ![]() .
.
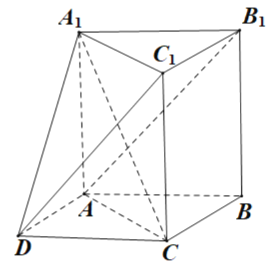
(1)若![]() ,证明:
,证明:![]() 四点共面,且
四点共面,且![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角.
所成角.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据三棱柱的性质及平行四边形性质,可证明四边形![]() 为平行四边形,则
为平行四边形,则![]() 四点共面;由
四点共面;由![]() 和
和![]() 可得四边形
可得四边形![]() 为正方形, 连接
为正方形, 连接![]() 交
交![]() 于
于![]() .在
.在![]() 中由余弦定理可得
中由余弦定理可得![]() ,进而可知
,进而可知![]() ,则可证明
,则可证明![]() 平面
平面![]() ,从而
,从而![]() .
.
(2)结合(1),建立空间直角坐标系,写出各个点的坐标,用![]() 表示出平面
表示出平面![]() 和平面
和平面![]() 的法向量,利用二面角
的法向量,利用二面角![]() 的余弦值为
的余弦值为![]() 求得
求得![]() 的值.由
的值.由![]() 的值可判断出
的值可判断出![]() 平面
平面![]() ,所以在正方形
,所以在正方形![]() 中即可求得直线
中即可求得直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
(1)证明:因为![]() 为直三棱柱,
为直三棱柱,
所以![]() ∥
∥![]() ,且
,且![]() ,
,
又因为四边形![]() 为平行四边形,
为平行四边形,
所以![]() ∥
∥![]() ,且
,且![]() ,
,
所以![]() ∥
∥![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
因为![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() ,所以四边形
,所以四边形![]() 为正方形,
为正方形,
连接![]() 交
交![]() 于
于![]() ,如下图所示:
,如下图所示:
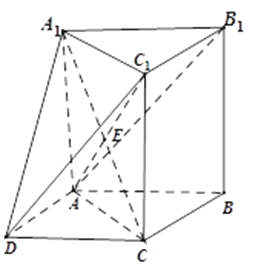
所以![]() ,在
,在![]() 中,
中,![]() ,
,![]()
在![]() 中由余弦定理得
中由余弦定理得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() ;
;
所以![]()
(2)由(1)知,可建立如下图所示的空间直角直角坐标系:
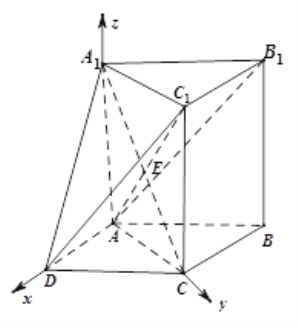
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由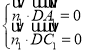 即
即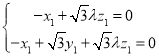 ,令
,令![]() ,可得
,可得![]()
设平面![]() 的法向量为
的法向量为![]()
由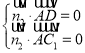 得
得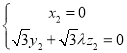 令
令![]() ,可得
,可得![]() ,
,
由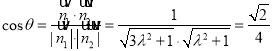
得![]() ,因为
,因为![]() ,所以
,所以![]()
此时![]() ,
,![]() ,所以四边形
,所以四边形![]() 为正方形,
为正方形,
因为![]() ,
,![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 与平面
与平面![]() 所成角为
所成角为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-lnx,g(x)=x2-ax.
(1)求函数f(x)在区间[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函数h(x)图像上任意两点,且满足![]() >1,求实数a的取值范围;
>1,求实数a的取值范围;
(3)若x∈(0,1],使f(x)≥![]() 成立,求实数a的最大值.
成立,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高三男生的体能达标情况,抽调了120名男生进行立定跳远测试,根据统计数据得到如下的频率分布直方图.若立定跳远成绩落在区间![]() 的左侧,则认为该学生属“体能不达标的学生,其中
的左侧,则认为该学生属“体能不达标的学生,其中![]() 分别为样本平均数和样本标准差,计算可得
分别为样本平均数和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
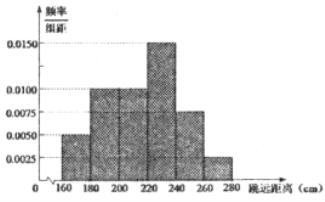
(1)若该校高三某男生的跳远距离为![]() ,试判断该男生是否属于“体能不达标”的学生?
,试判断该男生是否属于“体能不达标”的学生?
(2)该校利用分层抽样的方法从样本区间![]() 中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在
中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知南北回归线的纬度为![]() ,设地球表面某地正午太阳高度角为
,设地球表面某地正午太阳高度角为![]() ,
,![]() 为此时太阳直射纬度,
为此时太阳直射纬度,![]() 为该地的纬度值,那么这三个量之间的关系是
为该地的纬度值,那么这三个量之间的关系是![]() .当地夏半年
.当地夏半年![]() 取正值,冬半年
取正值,冬半年![]() 取负值,如果在北半球某地(纬度为
取负值,如果在北半球某地(纬度为![]() )的一幢高为
)的一幢高为![]() 的楼房北面盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离应不小于______(结果用含有
的楼房北面盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离应不小于______(结果用含有![]() 和
和![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由国家统计局提供的数据可知,2012年至2018年中国居民人均可支配收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均可支配收入 | 1.65 | 1.83 | 2.01 | 2.19 | 2.38 | 2.59 | 2.82 |
(1)求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)利用(1)中的回归方程,分析2012年至2018年中国居民人均可支配收入的变化情况,并预测2019年中国居民人均可支配收入.
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: 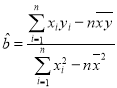 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点E,交棱
于点E,交棱![]() 于点F,则:
于点F,则:
①平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
②四边形![]() 一定是平行四边形;
一定是平行四边形;
③平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
④四边形![]() 的面积有最大值.
的面积有最大值.
其中所有正确结论的序号为( )
A.①④B.②③C.①②④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com